生存関数

生存関数（せいぞんかんすう、survival function）または生存時間関数とは、被験者、機器、またはその他の対象物が特定の時間を超えて生存する確率を与える関数である^[1][2]。

生存関数は、生存者関数（survivor function）^[3]または信頼性関数（reliability function）^[4]としても知られる。

信頼性関数という用語は、工学において一般的であり、生存関数という用語は、人間の死亡率を含むより広範囲のアプリケーションで用いられる。生存関数の別の名前は、相補累積分布関数（complementary cumulative distribution function、CCDF）である。

定義

T を区間 [0,∞) 上の累積分布関数 F(t) を持つ連続確率変数とする。その生存関数（または信頼性関数）は次のとおりである。

${\displaystyle S(t)=P(\{T>t\})=\int _{t}^{\infty }f(u)\,du=1-F(t).}$

生存関数の例

下のグラフは、仮想的な生存関数の例である。X軸は時間、Y軸は被験者の生存率である。このグラフは、被験者が時間 t を超えて生存する確率を示す。

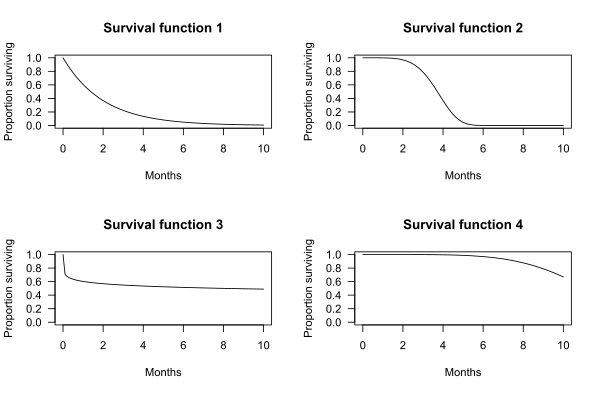
たとえば、生存関数1（survival function 1）の場合、t = 2ヶ月 より長く生存する確率は 0.37 である。つまり、被験者の 37% が 2か月 以上生存する。

生存関数2の場合、t = 2ヶ月 より長く生存する確率は 0.97 である。つまり、被験者の 97% が 2か月 以上生存する。

生存期間中央値（median survival）は、生存関数から求めることができる。たとえば、生存関数2の場合、被験者の 50% が 3.72か月 生存する。したがって、生存期間中央値は 3.72ヶ月 となる。

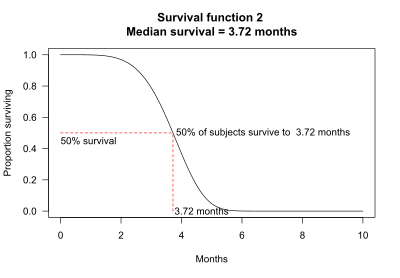
場合によっては、生存率中央値がグラフから判断できないこともある。たとえば、生存関数4では、50% 以上の被験者が10ヶ月の観察期間よりも長く生存する。

生存関数は、生存データを記述および表示するためのいくつかの方法の1つである。データを表示するもう1つの有用な方法は、被験者の生存期間の分布を示すグラフである。Olkinは著書^[5]（p.426）で、生存データの例として次のように述べている。空調設備の連続故障の間の時間数を記録した。連続した故障の間の時間は、1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246, 261 時間である。平均故障間隔は 59.6 である。この平均値は、データに理論的な曲線を当てはめるために使用される。次の図は、故障間隔の分布を示している。グラフの下にある青い目盛りは、連続した故障の間の実際の時間である。

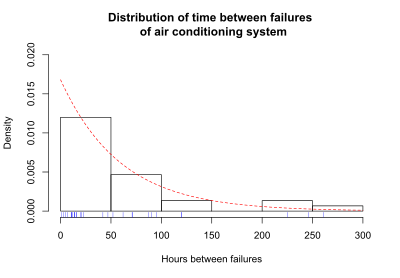
この故障時間の分布に、指数分布を表す曲線を重ねて示している。この例では、指数分布が故障時間の分布を近似している。指数曲線は、実際の故障時間に適合した理論上の分布である。この指数曲線は、λ（ラムダ）= 1/(平均故障間隔) = 1/59.6 = 0.0168 というパラメータで指定される。故障時間の分布は、時間が任意の正の値を取ることができる場合、確率密度関数（probability density function、PDF）と呼ばれる。方程式では、PDF を f(t) と表記する。時間が離散的な値（1日、2日、など）しか取れない場合、故障時間の分布は確率質量関数（probability mass function、PMF）と呼ばれる。ほとんどの生存分析法は、時間が任意の正の値をとると仮定し、f(t) を PDF としている。観測された空調設備の故障の間の時間を指数関数で近似すると、指数曲線から空調設備の故障時間の確率密度関数 f(t) が得られる。

生存データを表示するもう一つの有用な方法は、各時点までの累積故障数を示すグラフである。これらのデータは、各時点までの故障の累積数または累積故障率のいずれかで表示される。下のグラフは、空調設備の各時点での故障の累積確率（または割合）を示している。黒色の階段線は、累積故障率を示す。各段について、グラフの下部に、観測された故障時間を示す青色のマークがある。滑らかな赤線は、観測データに適合した指数曲線を表している。

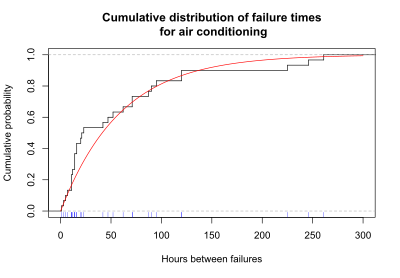
各時点までの累積故障率のグラフを累積分布関数（cumulative distribution function、CDF）と呼ぶ。生存分析では、累積分布関数は、生存期間が特定の時間 t 以下になる確率を示す。

T を生存期間とし、任意の正の数とする。特定の時間は小文字の t で示す。T の累積分布関数は次の関数で表される。

${\displaystyle F(t)=\operatorname {P} (T\leq t)}$

ここで、右辺は確率変数 T が t 以下になる確率を表す。時間が任意の正の値を取ることができる場合、累積分布関数 F(t) は、確率密度関数 f(t) の積分である。

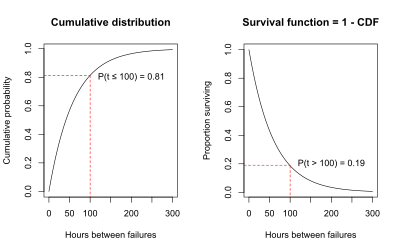
空調設備の例では、データに適合する指数曲線を用いて推定した場合、以下の CDF のグラフから、故障までの時間が100時間以下になる確率が 0.81 であることがわかる。

故障時間が100時間以下である確率をグラフ化する代わりに、故障時間が100時間を超える確率をグラフ化することもできる。確率の合計は 1 になる必要があるため、故障時間が100時間を超える確率は、1 から故障時間が100時間以下である確率を引いたものでなければならない。

これにより、

P(故障時間 > 100時間) = 1 - P(故障時間 < 100時間) = 1 - 0.81 = 0.19 となる。

この関係は、次のように、すべての故障時間に一般化される。

P(T > t) = 1 - P(T < t) = 1 – 累積分布関数

この関係を下のグラフに示す。左側のグラフは、累積分布関数で、P(T < t) である。右側のグラフは、P(T > t) = 1 - P(T < t) である。右側のグラフは、生存関数 S(t) である。S(t) = 1 – CDF である事実が、生存関数の別名が相補累積分布関数である理由である。

パラメトリックな生存関数

空調設備が好例であるが、生存期間の分布は、指数分布のような関数を使って高い精度で近似できる場合がある。生存分析では、指数分布、ワイブル分布、ガンマ分布、正規分布、対数正規分布、対数ロジスティック分布などといった分布が一般的に使用される^[4][6]。これらの分布は、パラメータによって定義される。たとえば，正規（ガウス）分布は、2つのパラメータ、つまり平均と標準偏差によって定義される。パラメータによって定義される生存関数は、パラメトリックであるという。

上記の4つの生存関数のグラフでは、生存関数の形状が特定の確率分布によって定義されている。生存関数1は指数分布、2はワイブル分布、3は対数ロジスティック分布、4は別のワイブル分布によって定義されている。

指数生存関数

指数型生存分布では、個人の年齢や機器の使用期間とは無関係に、どのタイミングでも死亡（故障）の確率は同じである。これはつまり、指数生存分布が無記憶性を持つということである。対象の生存期間は、その時点での死亡（故障）確率に影響しない。この指数関数は、部品が故障する際に交換されるようなシステムの寿命に適したモデルとなろう^[7]。また、短期における生体の生存のモデリングにも使い勝手が良いが、長期にわたる生体の生存のモデリングには適さないであろう^[8]。Efron and Hastie^[9]（p.134）では、「もし人間の寿命が指数分布に従っていると仮定すると、老人も若者もない。単に、運が良いか悪いかそれだけである」と述べている。

ワイブル生存関数

指数型生存関数における重要な仮定とは、危険率（hazard rate）が一定ということである。上記の例では、毎年死亡する男性の割合は10%で一定であり、これは危険率が定数であることを意味する。危険率が定数であるという仮定は、適切でないこともある。たとえば、ほとんどの生物では、死亡のリスクは中年期よりも老年期の方が大きく、つまり危険率は時間とともに増加するということである。また、乳がんのように、5年後に再発するリスクが低くなる疾患もある。これはつまり、危険率が時間とともに減少するということである。ワイブル分布は、指数分布を拡張して、危険率を定数にできるのはもちろん、増加、または減少するようにすることができる

他のパラメトリック生存関数

正規分布、対数正規分布、対数ロジスティックガンマ分布など、特定のデータセットへの適合度が高いパラメトリック生存関数は他にも存在する。個別具体的な応用段階でのパラメトリック分布の選択は、グラフィカルな方法や形式的な適合度検定を用いて行える。これらの分布と検定は、生存分析に関する教科書で説明されている^[1][2][4]。Lawlessの教科書は、パラメトリック・モデルを幅広くカバーしている^[10]。

パラメトリック生存関数は、観察期間以後の生存関数を推定できることが一つの理由となり、製造業への応用における使用が一般的である。ただし、パラメトリックな関数を適切に使用するには、選択した分布がデータに対してモデルとして良く適合している必要がある。適切な分布が使用できない場合、または臨床試験や実験の前に指定できない場合は、ノンパラメトリックな生存関数が代替手段として有用である。

ノンパラメトリック生存関数

生存のパラメトリック・モデルは、不可能または望ましくないかもしれない。このような状況で生存関数をモデル化する最も一般的な方法は、ノンパラメトリックなカプラン＝マイヤー推定量である。

特性

• すべての生存関数 ${\displaystyle S(t)}$ は単調減少、すなわち、すべての ${\displaystyle u>t}$ について ${\displaystyle S(u)\leq S(t)}$ である。
  • これは確率変数の特性であり、通常は、死亡率や何らかのシステムの故障に関連する一連の事象を時間にマッピングする。
• 時刻 ${\displaystyle t=0}$ は何らかの起源、通常は研究の開始またはあるシステムの運用開始を表している。${\displaystyle S(0)}$ は一般的に1であるが、システムが動作直後に故障する確率を表すために、これより少なくすることもできる。
• CDFは右連続関数（英語版）なので、生存関数 ${\displaystyle S(t)=1-F(t)}$ も右連続である。
• 生存関数は、確率密度関数 ${\displaystyle f(t)}$ と危険率関数 ${\displaystyle \lambda (t)}$ に関連づけられる。
  • ${\displaystyle f(t)=-S'(t)}$
  • ${\displaystyle \lambda (t)=-{d \over {dt}}\log S(t)}$

したがって、${\displaystyle S(t)=\exp[-\int _{0}^{t}\lambda (t')dt']}$ となる。

• 期待生存期間は、 ${\displaystyle \mathbb {E} (T)=\int _{0}^{\infty }S(t)dt}$ となる。

期待生存期間の公式の証明

確率変数 ${\displaystyle T\in [0,\infty )}$ の期待値は、次のように定義される。

${\displaystyle \mathbb {E} (T)=\int _{0}^{\infty }tf(t)dt}$

ここで、${\displaystyle f(t)}$ は確率密度関数である。また、${\displaystyle f(t)=-S'(t)}$ の関係を用いて、期待値の式を変形できる。

${\displaystyle \mathbb {E} (T)=-\int _{0}^{\infty }tS'(t)dt}$

これをさらに簡略化するには、部分積分を用いるとよい。

${\displaystyle -\int _{0}^{\infty }tS'(t)dt=-tS(t){\bigg |}_{0}^{\infty }+\int _{0}^{\infty }S(t)dt}$

定義により、${\displaystyle S(\infty )=0}$ であり、境界項はまったく0に等しいことを意味する。したがって、期待値は単に生存関数の積分であると結論づけることができる。

${\displaystyle \mathbb {E} (T)=\int _{0}^{\infty }S(t)dt}$

参照項目

• 故障率
• 超過頻度（英語版）
• カプラン＝マイヤー推定量
• 平均故障間隔
• 滞留時間 (統計学)（英語版）

脚注