共分散分析

共分散分析（きょうぶんさんぶんせき、analysis of covariance、ANCOVA）は、分散分析（ANOVA）と回帰を組み合わせた一般線形モデルである。共変量の効果をコントロールしながら、アウトカムの平均が、カテゴリカル独立変数である処置（treatment） の水準によらず等しいかを評価する。数学的には、アウトカムの分散を、共変量による分散、処置による分散、残差分散に分解する。共分散の群平均によってアウトカムを調整していると考えることもできる^[1]。

共分散分析では、${\displaystyle i}$ 番目の処置群での ${\displaystyle j}$ 番目の観測に関して、アウトカム ${\displaystyle y_{ij}}$ と共変量 ${\displaystyle x_{ij}}$ との間に線形関係を仮定する。

${\displaystyle y_{ij}=\mu +\tau _{i}+\beta \,(x_{ij}-{\overline {x}})+\epsilon _{ij}}$

アウトカムの総平均 ${\displaystyle \mu }$ と共変量のグローバル平均 ${\displaystyle {\overline {x}}}$ は観測データから導出される。処置効果 ${\displaystyle \tau _{i}}$、${\displaystyle \beta }$（回帰直線の傾き）、${\displaystyle \epsilon _{ij}}$ （未観測誤差項）をフィッティングする。

この仮定の下、処置効果の総和はゼロになる。

${\displaystyle \sum _{i}\tau _{i}=0}$

後述のように、線形回帰モデルの標準的な仮定が成立しているものとする^[2]。

使用法

検出力を上げる

ANCOVAは、群内の誤差分散を減らし、統計的検出力（群間差がある場合に、実際にその差が有意と判定される確率）を高めるため使用できる^[3]。これを理解するためには、F検定（群間差を評価する検定）を理解する必要である。 F検定では、群間分散を群内分散で割ることによって計算する。

${\displaystyle F={\frac {\mathrm {MS} _{\mathrm {between} }}{\mathrm {MS} _{\mathrm {within} }}}}$

この値が臨界値よりも大きければ、群間に有意差があると判断する。説明できない分散には、他の要因の影響だけではく、誤差分散（個人差など）も含まれる。共変量の影響は分母にまとめられる。共変量のアウトカムへの影響をコントロールすると、それが分母から除外されて F が大きくなり、検出力が大きくなる。

所与の差を調整する

ANCOVA のもう一つの使用法は、非等価群の所与の差を調整することである。割り付け前のアウトカムの群間差を修正することを目的とする。無作為割付が不可能な状況で、共変量によってスコアを調整し、比較可能性を高めるために使用される。しかし、群間差を消すことはできない。また、共変量と処置とが相関するため、共変量に関するアウトカムの分散を取り除くことで処置に関するアウトカムの分散まで取り除いてしまう可能性がある^[4]。

仮定

ANCOVAの使用の基礎となり、結果の解釈に影響を与える重要な仮定がある^[2]。標準的な線形回帰の仮定が保持され、共変量の傾きが全ての処置群で等しいと仮定する（回帰勾配の均一性）。

仮定1：回帰の線形性

アウトカムと変数との回帰関係は線形でなければならない。

仮定2：誤差分散の均一性

誤差は確率変数であり、さまざまな処置と観測に対して、平均がゼロで分散が等しい。

仮定3：誤差項の独立性

誤差は無相関である。すなわち、誤差の共分散行列は対角行列である。

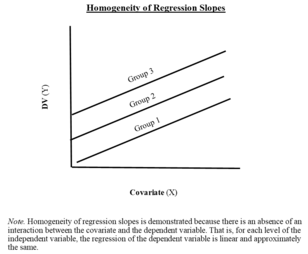
仮定4：誤差項の正規性

誤差（残差）は平均ゼロの正規分布に従う。

${\displaystyle \epsilon _{ij}\sim N(0,\sigma ^{2})}$

仮定5：回帰勾配の均一性

異なる回帰直線の傾きは同じである。すなわち、回帰直線はグループ間で平行である。

異なる回帰勾配の均一性に関する5番目の問題は、ANCOVAモデルの適切性を評価する上で特に重要です。また、正規分布する必要があるのは誤差項のみであることに注意してください。実際、ほとんどの場合、独立変数と付随変数の両方が正規分布しません。

ANCOVAの実施

多重共線性を検定する

共変量が別の共変量と強く相関する場合、統計的に冗長であるため、どちらか一方の共変量を削除する。

分散の均一性の仮定を検定する

誤差分散の均一性に関してルビーン検定を行う。共変量で調整した後の均一性が最も重要だが、調整前に均一なら、調整後も均一である可能性が高い。

回帰勾配の均一性を検定する

共変量と処置との相互作用を確認するために、相互作用項を含めたモデルを作成する。 相互作用が有意なら ANCOVA は実行すべきではない。Green らは、共変量で層別化して、アウトカムの群間差を評価することを提案している^[5]。

ANCOVA分析を実行する

回帰勾配の均一性が確認されたら、交互作用項なしで ANCOVA を実行する。この分析では、調整済み平均と調整済み平均二乗誤差を使用する。調整済み平均（最小二乗平均、LS平均、推定周辺平均、EMMとも呼ばる）は、アウトカムに対する共変量の影響をコントロールした後の群平均を指す。

フォローアップ分析

主効果が有意であった場合、いずれかの処置の水準間に有意差があることを意味する^[6]。どの水準が互いに有意に異なるかを正確に見つけるために、ANOVAの場合と同じフォローアップテストを使用できる。 処置が複数ある場合、相互作用がある可能性があります。これは、アウトカムに対する1つの処置の影響が、別の要因の水準に応じて変化することを意味する。階乗ANOVAと同じ方法を使用して、単純主効果を調査できる。

検出力に関する注意事項

従属変数の分散の一部を説明できる共変量を ANOVA に加えることで、統計的検出力が大きくことが期待される。しかし、追加した共変量が従属変数の分散をほとんど説明しない場合、自由度が減って検出力はむしろ小さくなる可能性もある。

関連項目

• 分散分析（ANOVA）
• 共分散の多変量分析（MANCOVA）

脚注

外部リンク

• Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares, and their analysis in R (University of Southampton)
• One-Way Analysis of Covariance for Independent Samples
• What is analysis of covariance used for?
• Use of covariates in randomized controlled trials by G.J.P. Van Breukelen and K.R.A. Van Dijk (2007)