差集合(さしゅうごう、英: set difference)とは、ある集合の中から別の集合に属する要素を取り去って得られる集合のことである[1]。特に、全体集合 U を固定して、U からその部分集合 A の要素を取り去って得られる集合を A の補集合という[2]。
定義
 差集合 B − A のベン図による視覚化(左が A、右がB。):
差集合 B − A のベン図による視覚化(左が A、右がB。):

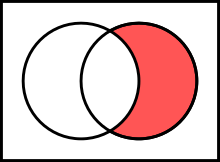
 差集合 A − B のベン図による視覚化(左が A、右がB。):
差集合 A − B のベン図による視覚化(左が A、右がB。):

集合 B から集合 A に属する元を間引いて得られる集合を

または B − A と表現し、B から A を引いた差、差集合あるいは B における A の(相対)補集合と呼ぶ。記号を用いて書けば、

すなわち

が差集合の定義である。これは A ∩ B とは限らない場合にも定義される。後述の補集合の言葉で書けば、 とは、B における A ∩ B の補集合である。なお、一般に集合の差は交換法則を満たさない:
とは、B における A ∩ B の補集合である。なお、一般に集合の差は交換法則を満たさない:

これらが等しくなるのは、 A = B のとき、またそのときに限る。
注意
集合 A, B が加法「+」を持つ代数的構造(特に加法群)の部分集合であるとき、 B − A は集合 {b − a | a ∈ A, b ∈ B} と紛らわしいので、この記法を使用する場合は注意が必要である。
また、LaTeXで入力するとき、差集合としては B \backslash A ( ) ではなく
) ではなく B \setminus A ( ) を用いるか[3][4]、
) を用いるか[3][4]、B \smallsetminus A ( ) を用いる[5][4]。
) を用いる[5][4]。
例
- P = {1, 3, 5, 7, 9} (10 以下の奇数の集合)
- Q = {2, 3, 5, 7} (10 以下の素数の集合)
このとき

であり、

である。
補集合
 補集合のベン図による視覚化(左がA、右がB。):
補集合のベン図による視覚化(左がA、右がB。):

全体集合や普遍集合[注釈 1]などと呼ばれる(大きな)集合 U を固定して、その部分集合についてのみ考えているとき(例えば、U が自然数全体、実数全体やある位相空間であるときなど) U の部分集合 A について、

を A の(絶対)補集合(ほしゅうごう)[注釈 2]といい、U が了解されている文脈では単に



のように表す。
- ある集合の補集合の補集合は、もとの集合自身である。
- 自然数について考えているとき、奇数全体の集合の補集合は偶数全体の集合である。
- 実数全体 R について考えているとき、有理数全体 Q の補集合
 は無理数全体である。
は無理数全体である。
注意
P の補集合を P c で表す場合、おおくは P が P の閉包(closure)を表す。逆に、P が補集合を表しているような文脈では、P c で P の閉包を記すことがある。
ド・モルガンの法則
P, Q をある集合の部分集合とするとき、

が成り立つことが分かる[6]。これはもっと一般化できて、 {Pλ}λ∈Λ をある基礎となる集合の部分集合の族とするときに、

が成り立つ。これらをド・モルガンの法則という。
この法則は、対応する論理記号の性質(特に双対性)を反映したものである。詳しくは数理論理学の項目を参照。
関連項目
注釈
- ^ 英: universe
- ^ 英: complement
出典
- ^ "差集合". ブリタニカ国際大百科事典 小項目事典. コトバンクより2022年2月15日閲覧。
- ^ "補集合". ブリタニカ国際大百科事典 小項目事典. コトバンクより2022年2月15日閲覧。
- ^ Knuth, D. (1986). The TeXbook. Addison–Wesley. p. 436. ISBN 0-201-13447-0
- ^ a b 小田忠雄「数学の常識・非常識:由緒正しいTeX入力法」(PDF)『数学通信』第4巻第1号、1999年5月、95–112頁。
- ^ “Users’ guide to the fonts (for version 2.2d)”. CTAN. p. 20. 2023年11月7日閲覧。
- ^ 丹下基生『SGCライブラリ-163 例題形式で探求する集合・位相(連続写像の織りなすトポロジーの世界)』サイエンス社、2020年、p.6
参考文献





























