Równanie kwadratowe
| | Ten artykuł wymaga uzupełnienia informacji. Artykuł należy uzupełnić o istotne informacje: historia, bardziej bezpośrednie odwołanie do funkcji kwadratowej (metoda graficzna), ogólniej o rezolwentach Lagrange’a (teraz połączone ze wzorami Viète’a), metody numeryczne (uwarunkowania), wprost o postaci monicznej (a = 1), pełniej o różnych ciałach (w tym charakterystyki 2 i rozszerzeniach; opisanie symbolu pierwiastka w ich kontekście). Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu. |
 | Ten artykuł dotyczy równań kwadratowych i ich rozwiązań. Zobacz też: funkcja kwadratowa, gdzie opisano wielomiany kwadratowe w szerszym kontekście. |

Równanie kwadratowe, równanie drugiego stopnia[potrzebny przypis] – równanie algebraiczne z jedną niewiadomą w drugiej potędze i opcjonalnie niższych, czyli postaci[1]:
Wielkości są znane jako współczynniki, kolejno: kwadratowy, liniowy i stały bądź wyraz wolny[2]. Założenie oznacza, że do równań kwadratowych nie zalicza się równań liniowych.
Niewiadoma i współczynniki w równaniu kwadratowym mogą być liczbami rzeczywistymi, zespolonymi bądź elementami dowolnego innego pierścienia. Równania te należą do wielomianowych, a konkretniej są równaniami wielomianowymi drugiego stopnia.
Rozwiązania
 Zobacz też: równanie i wielomian.
Zobacz też: równanie i wielomian.
Rozwiązaniem równania kwadratowego
nazywa się każdą liczbę, która podstawiona w miejsce daje po wykonaniu wszystkich działań równość. Jeżeli przedstawić powyższe równanie w postaci iloczynowej, tzn.
dla pewnych liczb to jego rozwiązaniem jest dowolna z liczb gdyż podstawiona zamiast sprawia, że lewa strona równości jest równa zeru.
W szczególności może być wówczas postacią iloczynową równania wyjściowego jest
Wyróżnik
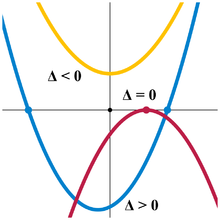
■ <0: x2 + 1⁄2
■ =0: −4⁄3x2 + 4⁄3x − 1⁄3
■ >0: 3⁄2x2 + 1⁄2x − 4⁄3
 Zobacz też: wyróżnik.
Zobacz też: wyróżnik.
Ponieważ
(piąta równość zachodzi na podstawie wzoru skróconego mnożenia na różnicę kwadratów), to pierwiastkami tego wielomianu są wielkości
oraz
Wyrażenie
nazywa się wyróżnikiem równania kwadratowego. W szczególności jeżeli to
Powyższe równości są prawdziwe w dziedzinie zespolonej – w szczególności, gdy to
gdzie jest jednostką urojoną, a wyrażenie pod pierwiastkiem po prawej stronie jest dodatnią wielkością rzeczywistą. Wtedy też równanie ma dwa sprzężone ze sobą rozwiązania zespolone, których część rzeczywista wynosi Jeżeli to rozwiązaniami są liczby rzeczywiste symetryczne względem Przypadki dla można podsumować zdaniem: średnia arytmetyczna pierwiastków wynosi (por. wzory Viète’a).
Równanie kwadratowe ma rozwiązanie w dziedzinie rzeczywistej, o ile Dokładniej, jeśli:
- to równanie ma dwa rozwiązania rzeczywiste (dwa pierwiastki rzeczywiste),
- to równanie ma jedno rozwiązanie rzeczywiste (podwójny pierwiastek rzeczywisty),
- to równanie nie ma rozwiązań rzeczywistych.
Rozwiązania korzystające z wyróżnika są poprawne także nad skończonymi ciałami gdzie jest pewną liczbą pierwszą większą od 2[potrzebny przypis].
- Przykłady
- Równanie
- ma dwa rozwiązania, gdyż jego wyróżnik jest równy
- Są nimi oraz
- Równanie
- po uporządkowaniu ma postać
- Nie ma rozwiązań rzeczywistych, gdyż
- jednak ma rozwiązania zespolone: ponieważ to rozwiązania mają postać
- Równanie
- ma jedno rozwiązanie gdyż wyróżnik
Wzory skróconego mnożenia
 Zobacz też: wzory skróconego mnożenia.
Zobacz też: wzory skróconego mnożenia.
Równania kwadratowe można niekiedy przedstawić w postaci iloczynowej wprost ze wzorów skróconego mnożenia.
- Przykłady
- Równanie
- można zapisać korzystając ze wzoru skróconego mnożenia na kwadrat sumy jako
- wtedy jest jedynym rozwiązaniem spełniającym powyższą równość.
- Ze wzoru skróconego mnożenia na różnicę kwadratów równanie
- jest tożsame równaniu
- skąd musi być
- lub
- tzn. rozwiązaniami jest każda z liczb
- oraz
Wzory Viète’a
 Zobacz też: wzory Viète’a.
Zobacz też: wzory Viète’a.
Znając jedno rozwiązanie, można wskazać drugie, korzystając z tzw. wzorów Viète’a, które dla wielomianu mają postać
Przykładem ich zastosowania może być następujący przypadek szczególny: jeżeli współczynniki wielomianu
spełniają równości i to można go zapisać jako
Oznacza to, że rozwiązaniami równania
którego współczynniki spełniają powyższe tożsamości są liczby
- oraz
- Przykłady
- Równanie
- daje się przedstawić w postaci
- skąd otrzymuje się rozwiązania
- oraz
- Równanie
- można zapisać jako
- co oznacza, że rozwiązaniami są liczby
- oraz
Dopełnianie do kwadratu
Zwykle wykorzystanie wzorów skróconego mnożenia nie jest możliwe, jednak czasami drobne przekształcenia równania pozwalają uprościć proces wyznaczania rozwiązania; szczególnie, jeśli wyłącznie wyraz wolny stanowi przeszkodę. Niech
będzie równaniem, którego rozwiązania są poszukiwane. Jeżeli
to wyjściowe równanie można przekształcić następująco:
skąd
a skorzystawszy ze wzoru skróconego mnożenia na różnicę kwadratów otrzymuje się
co daje rozwiązania
- oraz
Podobnie jak objaśniono to wyżej, rozwiązanie rzeczywiste istnieje wyłącznie, gdy
- Przykłady
- Równanie
- jest tożsame następującemu
- kontynuując uzyskuje się
- co jest równoważne
- oraz
- a więc rozwiązaniami są
- oraz
Współczynniki całkowite
Istnieje prosta metoda wyznaczania pierwiastków wymiernych równania kwadratowego o współczynnikach całkowitych, czyli postaci
gdzie są liczbami całkowitymi (jeżeli są liczbami wymiernymi, spośród których choć jedna nie jest całkowita, to równanie można pomnożyć stronami przez najmniejszą wspólną wielokrotność mianowników tych współczynników uzyskując równanie równoważne, tj. o jednakowym zbiorze rozwiązań). Dokładniej:
- Jeżeli liczba wymierna gdzie i są względnie pierwszymi liczbami całkowitymi (tzn. ich największy wspólny dzielnik jest równy 1) jest pierwiastkiem powyższego, to jest dzielnikiem a jest dzielnikiem
Powyższe twierdzenie jest prawdziwe także dla wielomianów wyższych stopni.
- Przykłady
- Rozwiązaniami wymiernymi równania
- mogą być tylko liczby należące do zbioru Podstawiając otrzymuje się wyraźnie dużą liczbę dodatnią po lewej stronie; podstawienie daje liczba podstawiona do równania daje po lewej stronie wartość liczba jest rozwiązaniem powyższego równania (drugim jest ).
Inne
Jeżeli suma współczynników równania
jest równa zeru, tzn. to wśród jego rozwiązań znajduje się liczba (por. przykład z powyższej sekcji). Jeżeli to liczba jest pierwiastkiem tego równania.
- Przykład
- Równanie
- na mocy powyższego faktu ma pierwiastek równy
Zobacz też
 | Zobacz publikację Równania kwadratowe w Wikibooks |
Przypisy
Linki zewnętrzne
- Eric W.E.W. Weisstein Eric W.E.W., Quadratic Equation, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-12-16].
 Quadratic equation (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-12-16].
Quadratic equation (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-12-16].
- p
- d
- e
| pojęcia definiujące | |||||||
|---|---|---|---|---|---|---|---|
| typy | |||||||
| pojęcia podstawowe | |||||||
| opis algebraiczny |
| ||||||
| opis parametryczny |
| ||||||
| występowanie |
| ||||||
| powiązane powierzchnie |
| ||||||
| nawiązujące pojęcia |
| ||||||
| uogólnienia | |||||||
| badacze |

- p
- d
- e

- PWN: 3929541
- Britannica: topic/quadratic-equation











































































































