結合法則

数学における結合性（けつごうせい、英: associative property^[1],associativity）は、一部の二項演算がもつ性質である。演算が結合的であるための必要十分条件を結合法則（けつごうほうそく、英: associative law; 結合律、結合則）という。命題論理において、結合則（結合規則）は形式的証明における式に対する妥当（英語版）な置換規則（英語版）のひとつに挙げられる。

同一式にて同じ結合的演算が複数回現れる場合、それらの演算を施す順番は、被演算子の順序を変えない限り、結果に影響しない。つまり、（必要ならば中置記法と括弧を使った式に書き換えて）括弧の位置を入れ替えても、式の値は変わらない。例えば、

• ${\displaystyle (2+3)+4=2+(3+4)=9}$
• ${\displaystyle 2\times (3\times 4)=(2\times 3)\times 4=24}$

を例にとると、各行とも左辺と中辺で括弧の位置が変わっている（そして被演算子の現れる位置は変わっていない）けれども、その値である右辺は変わりないことを述べている。このような関係式は、被演算子を任意の実数とする加法や乗法を計算する限りにおいて満足されるから、それを「実数の加法および乗法は結合的（演算）である」とか、「実数の加法および乗法は（実数全体の成す集合上で）結合法則を満足する」などと言い表す。

結合性は、「二つの被演算子の現れる位置を入れ替えても結果が変わらない」ことを意味する可換則とは異なる。例えば、実数の乗法が可換演算であるのは、実数の乗法において被演算子の順番を変えてもよいこと—つまり a × b = b × a—が満足されることによる。

結合的演算は数学において遍く存在する。事実として、多くの代数的構造（例えば半群や圏）では、それらの持つ二項演算が結合的であることを明示的に要請される。

とはいえ、重要で意義のある非結合的演算もたくさん存在する。例えば減法、冪演算、ベクトルの交叉積などはそうである。

定義

厳密に、集合 S 上で定義された二項演算 ∗ が結合的であるとは、結合法則

を満足するときに言う。ここで、∗ は考えたい演算（それを一般に「乗法」や「積」と呼んだりする^{[注釈 1]}）を表す記号（演算子）であって、これは別にどのような記号が用いられてもよいし、あまつさえ「乗法」を表す記号のない併置 (juxtaposition) 記法で と書くこともある。

結合法則を函数記法で表すこともでき、その場合は

のようになる。

一般化された結合法則

二項演算が結合的ならば、その演算が反復して適用されるとき、その式においてきちんと（開きと閉じが）対になる括弧がどのように挿入されるかを気にすることなく、その演算結果が同じであることがわかる^[2]。そのことを一般化された結合法則 (generalized associative law) と言う。実例として、四つの元の積を、それらの因子の順番を変えることなく書き下せば、五種類の異なる計算順序が考えられる:

• ${\displaystyle ((ab)c)d,}$
• ${\displaystyle (ab)(cd),}$
• ${\displaystyle (a(bc))d,}$
• ${\displaystyle a((bc)d),}$
• ${\displaystyle a(b(cd)).}$

が、これらの積を得る演算が結合的ならば、一般化された結合法則の述べるに従い、これらすべてが同じ値の積であることが結論される。となれば（これらの式から括弧をすべて取り払った式に既に別の意味が施されているのでない限り）この積において括弧は「不要」のものと考えることができて、この積を紛れの虞なく

と書くことができる。

このような繰り返しの積において、因子となる元の数が増えるにしたがって、釣り合いのとれた括弧の挿入の仕方の総数は急速に増加するけれども、演算が結合的ならばそれらの区別もやはり必要がなくなる。

結合的だからといって単純に括弧を取り去ってはいけない例として、双条件（英語版） ↔ を挙げよう。↔ は結合的であって A ↔ (B ↔ C) は (A ↔ B) ↔ C に同値であるが、A ↔ B ↔ C はふつうは A ↔ B かつ B ↔ C の意味であって先のふたつとは同値でない。

例

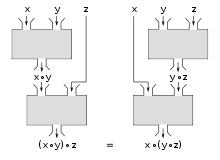
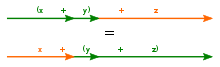
結合的演算の例をいくつか挙げる:

• 文字列結合。3つの文字列 "a"、"b"、"c" を繋げる際、先の2つを繋いで "ab" を得てから、その末尾に3つめの "c" を繋ぐと、"abc" となる。一方で、後の2つを繋いで "bc" を得てから、その先頭に1つめの "a" を繋いでも、同じく "abc" となる。そのため、文字列結合は結合的である。なお、可換ではない。

• 複素数同士の加法。（複素数とは、実数と虚数の総称であり、いわゆる数。）グループ化を表す括弧は、曖昧さを生まずに除去できる。

${\displaystyle (x+y)+z=x+(y+z)=x+y+z}$

• 複素数同士の乗法。グループ化を表す括弧は、曖昧さを生まずに除去できる。

${\displaystyle (xy)z=x(yz)=xyz}$

• 右自明演算 ${\displaystyle x*y=x}$（必ず ${\displaystyle x}$ の値を返す）、および左自明演算 ${\displaystyle x}$ ∘ ${\displaystyle y=y}$（必ず ${\displaystyle y}$ の値を返す）。どちらも可換ではない。

• 複素数および四元数の加法および乗法。

• 八元数の加法。なお、乗法は結合的でない。

• 最大公約数をとる演算。

${\displaystyle \operatorname {gcd} (\operatorname {gcd} (x,y),z)=\operatorname {gcd} (x,\operatorname {gcd} (y,z))=\operatorname {gcd} (x,y,z)\qquad (\forall x,y,z\in \mathbb {Z} )}$

• 最小公倍数をとる演算。

${\displaystyle \operatorname {lcm} (\operatorname {lcm} (x,y),z)=\operatorname {lcm} (x,\operatorname {lcm} (y,z))=\operatorname {lcm} (x,y,z)\qquad (\forall x,y,z\in \mathbb {Z} )}$

• 集合の交叉および合併:
  $${\displaystyle {\begin{array}{l}(A\cap B)\cap C=A\cap (B\cap C)=A\cap B\cap C\\(A\cup B)\cup C=A\cup (B\cup C)=A\cup B\cup C\end{array}}\qquad (\forall A,B,C).}$$

  

• 適当な集合 M に対する M 上の自己写像（写像 M → M）全体の成す集合 S ≔ M^Mについて、S 上で定義された合成演算 ∘ は結合的である:
  $${\displaystyle (f\circ g)\circ h=f\circ (g\circ h)=f\circ g\circ h\qquad (\forall f,g,h\in S).}$$

  

• 少し一般に、四つの集合 M, N, P, Q とそれらの間の写像 h: M → N, g: N → P, f: P → Q についてやはり
  $${\displaystyle (f\circ g)\circ h=f\circ (g\circ h)=f\circ g\circ h}$$

  
  が成り立つ。要するに写像の合成は常に結合的である。

• 三元集合 {A, B, C} に演算を以下の乗積表に従って定めたものは結合的である（かつ可換でない）:

×	A	B	C
A	A	A	A
B	A	B	C
C	A	A	A

• 通常の行列の積は結合的である。行列は線型写像を表現し、行列の積は線型写像の合成に対応するから、合成について既に見たことから行列の積の結合性は直ちに得られる^[3]。

命題論理

演繹の推論規則
命題計算
モーダスポネンス モーダストレンス モーダスポネンストレンス（英語版） 連言導入 簡単化 選言導入 選言除去 選言三段論法 仮言三段論法 構成的ジレンマ（英語版） 破壊的ジレンマ（英語版） 二条件導入（英語版） 二条件除去（英語版）
述語計算
普遍汎化 普遍例化 存在汎化 存在例化
カテゴリ:推論規則
表 話 編 歴

結合規則

標準的な真理函数的命題論理において、結合則 (association^[4][5], associativity^[6]) は二つの妥当（英語版）な置換規則（英語版）を言う。それは、論理学的証明における論理式に現れる括弧の位置を動かしてもよい規則を述べるもので、論理結合子を用いて書けば

• ${\displaystyle (P\lor (Q\lor R))\iff ((P\lor Q)\lor R)}$
• ${\displaystyle (P\land (Q\land R))\iff ((P\land Q)\land R),}$

のふたつである。ただし、"${\displaystyle \iff }$" はメタ論理（英語版）の記号（英語版）で、「形式的証明において置換してよい」ことを表す。

論理演算の結合性

真理函数的命題論理における真理函数の結合子のいくつかは結合性 (associativity) を持つ。以下の論理同値（英語版）（これらは真理函数的恒真式である）は結合性が特定の結合子の持つ性質であることを示している ^[7]:

選言の結合性

${\displaystyle ((P\lor Q)\lor R)\leftrightarrow (P\lor (Q\lor R))}$

${\displaystyle (P\lor (Q\lor R))\leftrightarrow ((P\lor Q)\lor R)}$

連言の結合性

${\displaystyle ((P\land Q)\land R)\leftrightarrow (P\land (Q\land R))}$

${\displaystyle (P\land (Q\land R))\leftrightarrow ((P\land Q)\land R)}$

論理同値の結合性

${\displaystyle ((P\leftrightarrow Q)\leftrightarrow R)\leftrightarrow (P\leftrightarrow (Q\leftrightarrow R))}$

${\displaystyle (P\leftrightarrow (Q\leftrightarrow R))\leftrightarrow ((P\leftrightarrow Q)\leftrightarrow R)}$

接合否定 (joint denial) は結合的でない真理函数結合子の例である。

非結合的演算

集合 S 上の二項演算 ∗ が結合法則を満足しない—記号で書けば

—となるとき、非結合的 (non-associative) である、必ずしも結合的でないなどという。

そのような演算では、計算順序は結果に影響する。非結合演算の例として

• 減法: ${\textstyle (5-3)-2\neq 5-(3-2)}$
• 除法: ${\textstyle (4/2)/2\neq 4/(2/2)}$
• 冪演算: ${\textstyle 2^{(1^{2})}\neq (2^{1})^{2}}$

などがある。あるいは無限和もまた一般には非結合的である。例えば:

非結合的構造の研究は、古典代数学の主流からはいくらか異なった理由から生じてくるものである。非結合多元環の領域にあってすでに一大分野へと発展したリー代数の理論では、結合法則の代わりにヤコビ恒等式が採用される。リー代数は無限小変換（英語版）の本質的な特質を抽象化するものであり、数学に遍在するものとなった。

既に深く調べられているほかの特定種類の非結合的構造もあり、それらは何らかの特定の応用から、あるいは組合せ論のような分野から生じたものである。その他の例は、Quasigroup（英語版）、準体（英語版）、非結合的環、非結合的多元環、可換（非結合的）マグマ（英語版）など。

非結合的演算の記法

非結合的演算が一つの式の中で複数回現れるときには、評価の順を指し示すために括弧を挿入することは（例えば 2/3/4 のように、ほかの方法で順番を指定する記法を用いているのでない限り）一般には不可避である。とはいえ、いくつかのよく用いられる非結合的演算については、特定の順番に評価することにして括弧の使用を回避する簡便記法が、受け入れられている。

左結合 (left-associative) 演算とは、規約として左から右に評価する—式で書けば

を意味する—演算を言う。同様に右結合 (right-associative) 演算は、右から左に評価するものと約束する: 左結合演算も右結合演算もどちらも生じ得る。左結合演算の例:

• 実数の減法および除法^{[8][9][10][11][12]}:
  $${\displaystyle x-y-z:=(x-y)-z}$$

  
  $${\displaystyle x/y/z:=(x/y)/z.}$$

  
• 函数の適用:
  $${\displaystyle (f\,x\,y)=((f\,x)\,y).}$$

  
  この記法はカリー化の同型によって動機づけられる。

右結合演算の例:

• 実数の冪（上付き添字記法の場合）:
  $${\displaystyle x^{y^{z}}=x^{(y^{z})}.}$$

  
  冪演算は、反復的な左結合冪演算にあまり需要がない（左からの繰り返しの冪は、冪指数の乗法を使って
  $${\displaystyle (x^{y})^{z}=x^{(yz)}}$$

  
  と書き直せる）ため、括弧が付かない場合にはふつう右結合的とする。
  • 正しく組まれている限り、上付き添字それ自体に括弧で括るのと本質的に同じ効果が期待できる。例えば 2^x+3 という式では右肩の和の計算が冪をとるよりも先に行われ、それは括弧で括って 2^(x+3) と明示的に書いたときに期待される計算順序になっている。それゆえ、x^yz のような式が与えられたときは、底 x に対する全体の冪指数 y^z がまず計算されるのは必定である。とはいえ、手書きする場合などは特にそうだが、文脈によっては
    $${\displaystyle {x^{y}}^{z},\quad x^{yz},\quad x^{y^{z}}}$$

    
    （これらを、陽に括弧を付けて書けば、順に ${\textstyle (x^{y})^{z},\,x^{(yz)},\,x^{(y^{z})}}$）の判別が難しいこともある。そういった場合には、ふつう右結合性が暗黙に用いられている。
• 写像の合成（図式順）:
  $${\displaystyle \mathbb {Z} \rightarrow \mathbb {Z} \rightarrow \mathbb {Z} =\mathbb {Z} \rightarrow (\mathbb {Z} \rightarrow \mathbb {Z} )}$$

  
  $${\displaystyle x\mapsto y\mapsto x-y=x\mapsto (y\mapsto x-y).}$$

  
  これらの演算の右結合記法は、カリー–ハワード対応およびカリー化同型に動機づけられる。

評価順について特定の規約がない演算の例:

• 実数の冪演算（中置記法の場合）:^[13]
  $${\displaystyle (x^{\wedge }y)^{\wedge }z\neq x^{\wedge }(y^{\wedge }z).}$$

  
• クヌースの矢印記法:
  $${\displaystyle {\begin{array}{l}a\uparrow \uparrow (b\uparrow \uparrow c)\neq (a\uparrow \uparrow b)\uparrow \uparrow c\\a\uparrow \uparrow \uparrow (b\uparrow \uparrow \uparrow c)\neq (a\uparrow \uparrow \uparrow b)\uparrow \uparrow \uparrow c\\{\text{etc.}}\end{array}}}$$

  
• ベクトルの交叉積（ベクトル三重積）:
  $${\displaystyle {\vec {a}}\times ({\vec {b}}\times {\vec {c}})\neq ({\vec {a}}\times {\vec {b}})\times {\vec {c}}\qquad (\exists {\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{3}).}$$

  
• 実数の対ごとの算術平均:
  $${\displaystyle {(x+y)/2+z \over 2}\neq {x+(y+z)/2 \over 2}\qquad (\forall x,y,z\in \mathbb {R} ,x\neq z).}$$

  
• 集合の差: ${\displaystyle (A\setminus B)\setminus C}$ は ${\displaystyle A\setminus (B\setminus C)}$ と一致しない（論理学における否定論理包含（英語版）の場合と比較せよ）。

プログラミング言語

中置記法を採用しているプログラミング言語においては、任意の演算子について数学で言うところの結合法則が成り立たないことを仮定して、その式の意味をどういった順序で、値を演算子により結合させたものとするかについて、それぞれの言語にそれぞれ法則がある。「演算子の優先順位」(英: Operator precedence) と「演算子の結合性（英語版）」（英: Operator associativity) と言う。

なお、優先順位と結合性は値の扱いに関する規則であって、式の評価の順序に関する規則ではないことに注意が必要である。評価順は優先順位と結合性に直感的に従っていることもあれば、従っていないこともある。言語仕様としては決められていないこともある（評価順と関連するものとして、短絡評価がある。短絡評価のためには評価順が決まっている必要があるため、一般に演算子の左辺と右辺の評価順を決めていないC言語だが、短絡評価される演算子については決まっている。Javaは仕様で全て決めている。Adaでは両辺を評価する演算子と短絡評価の演算子とが用意されている。）。

優先順位と結合性は、仕様上の表現としては構文規則の一部として決まっているものが多い（たいていは便利さのために別表にまとめられている。yaccのように通常の規則とは別建てで定義できるものもある）。ここでは例として、四則演算を主に挙げるが、他の演算子についても規則は同様にある。

優先順位

（ここでの前提である、中置記法を採用している）たいていのプログラミング言語の四則演算の演算子において、加減算より乗除算のほうが優先順位が高い、としているものが多い。

すなわち a * b + c は (a * b) + c という意味であり、a - b / c は a - (b / c) という意味である。

多くの演算子を持ち、その数に応じて多くの優先順位を定めているC言語のような言語もあれば、ほとんど優先順位が無く、次節で説明する結合性のみで、どんな演算も左から右、あるいは右から左（たとえばAPL）といったように決めている言語もある。

結合性

（前節と同様、中置記法を採用している）たいていのプログラミング言語の四則演算の演算子において、加算と減算、乗算と除算のそれぞれの間には優先順位に差が無い。加減算の連続、たとえば a + b - c + d - e というような式は、左から順に (((a + b) - c) + d) - e という意味となる。このような結合を"左結合" (英: left-associative)、あるいは"左から右" (英: left to right) と言う。逆が"右結合"（英: right-associative)、あるいは"右から左" (英: right to left) である。

右結合の例としては、C系の言語に特徴的な代入演算子 = は右結合である。a = b = 1; という式文における式は a = (b = 1) という意味であり b = 1 という代入演算子による式の値は 1 なので、それが a に(も)代入され、結果として a と b に 1 が代入される。

冪乗の演算子として ** や ^ がある言語があるが、数学の記法では ${\displaystyle a^{b^{c}}}$ と ${\displaystyle (a^{b})^{c}}$ のように、左を先にしたい場合に括弧が要るので、右結合すなわち a**b**c は a**(b**c) という意味であるとしたほうが数学の記法とは一致するが（たとえばRubyでは ** は右結合である（オブジェクトの種類等によるものではなく、構文上の規則である））、VBのように算術演算は全て左結合としているため冪乗の ^ も左結合^[14]、という言語もある。

非結合（non-associative）は、右結合でも左結合でもない、たとえば比較演算子 < のように、a < b < c の意味が (a < b) < c でも a < (b < c) でもない、というような演算子の結合性である（C言語では左結合として解釈し、比較結果の真理値を整数0か1として、次の比較を行うという通常は意図しない意味を持ってしまう。Pythonのように a < b < c と書いて、意図した通りの意味になる言語もある）。加算や乗算のみの演算のような順序によらない演算には順序を定めない、という言語も考えられるが、あまり見られない（算術と違いコンピュータ上の計算ではオーバーフロー等のために、真に順序によらない計算は実はあまりない、という事情もある）。

関連項目

• ライトの結合性判定法（英語版）
• 畳み込み級数: 級数の中間項が打ち消しあうには加法の結合性が必要
• 半群: 結合的二項演算を持つ集合
• 可換性・分配性: 結合性と同様に、二項演算にしばしば期待されるよい性質
• 冪結合性（英語版）・交代性（英語版）・柔軟性（英語版）・多項結合性（英語版）: 弱い形の結合性
• モーファンク恒等式（英語版）からも弱い形の結合性が出る

注

注釈

出典

外部リンク

• Weisstein, Eric W. "Associative". mathworld.wolfram.com (英語).
• associativity in nLab
• associative - PlanetMath.（英語）
• Definition:Associative Operation at ProofWiki
• Category:Definitions/Associativity at ProofWiki
• Ivanova, O.A.; Smirnov, D.M. (2001), “Associativity”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Associativity