アーラン分布

アーラン分布

確率密度関数
累積分布関数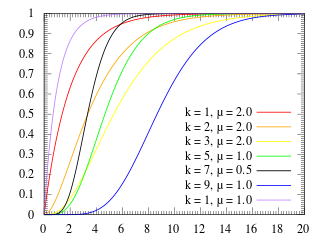
母数	${\displaystyle k\in \mathbb {N} }$ 形状母数（英語版）（自然数） ${\displaystyle \mu >0}$ 尺度母数（英語版）（実数） または、${\displaystyle \lambda =1/\mu >0}$ 比（実数）
台	${\displaystyle [0,\infty )}$
確率密度関数	${\displaystyle {\frac {1}{(k-1)!\,\mu ^{k}}}x^{k-1}e^{-x/\mu }}$ ${\displaystyle ={\frac {\lambda ^{k}}{(k-1)!}}x^{k-1}e^{-\lambda x}}$
累積分布関数	${\displaystyle 1-e^{-x/\mu }\sum _{n=0}^{k-1}{\frac {1}{n!}}\left({\frac {x}{\mu }}\right)^{n}}$ ${\displaystyle =1-e^{-\lambda x}\sum _{n=0}^{k-1}{\frac {(\lambda x)^{n}}{n!}}}$
期待値	${\displaystyle k\mu ={\frac {k}{\lambda }}}$
中央値	単純な閉形式を持たない
最頻値	${\displaystyle (k-1)\mu ={\frac {k-1}{\lambda }}\ {\text{ for }}k\geq 1}$
分散	${\displaystyle k\mu ^{2}=k/\lambda ^{2}}$
歪度	${\displaystyle 2/{\sqrt {k}}}$
尖度	${\displaystyle 6/k}$
エントロピー	${\displaystyle k+\ln \mu +\sum _{n=1}^{k-1}\ln n+(1-k)\psi (k)}$ ${\displaystyle =k-\ln \lambda +\sum _{n=1}^{k-1}\ln n+(1-k)\psi (k)}$
モーメント母関数	${\displaystyle {\frac {1}{(1-\mu \,t)^{k}}}=\left({\frac {\lambda }{\lambda -t}}\right)^{k}}$ ${\displaystyle {\text{ for }}t<1/\mu =\lambda }$
特性関数	${\displaystyle {\frac {1}{(1-i\mu t)^{k}}}=\left({\frac {\lambda }{\lambda -it}}\right)^{k}}$
テンプレートを表示

アーラン分布（アーランぶんぷ、英: Erlang distribution）は、待ち行列の待ち時間を計算するためにデンマークの数学者アーランが提唱した確率分布であり、特に通信トラフィック工学で使われる。

定義と性質

アーラン分布は2つの母数 k（正の整数）および μ（正の実数）によって定まり、その確率密度関数は次のように定義される。

${\displaystyle f(x;k,\mu )={\frac {1}{(k-1)!\,\mu ^{k}}}x^{k-1}e^{-x/\mu }\quad {\text{for }}x>0}$

等価な定義として、パラメータ λ = 1/μ を用いて次のように表されることもある。

${\displaystyle f(x;k,\lambda )={\frac {\lambda ^{k}}{(k-1)!}}x^{k-1}e^{-\lambda x}\quad {\text{for }}x>0}$

アーラン分布の累積分布関数は、以下のように求められる。

${\displaystyle {\begin{aligned}F(x)&=\int _{0}^{x}f(t;k,\mu )\,dt=1-e^{-x/\mu }\sum _{n=0}^{k-1}{\frac {1}{n!}}\left({\frac {x}{\mu }}\right)^{n}\\&=\int _{0}^{x}f(t;k,\lambda )\,dt=1-e^{-\lambda x}\sum _{n=0}^{k-1}{\frac {(\lambda x)^{n}}{n!}}\end{aligned}}}$

定義より（あるいは後述する指数確率変数を用いた解釈により）期待値 E[X] および分散 V[X] は以下のようになる。

${\displaystyle E[X]=k\mu ={\frac {k}{\lambda }},\,\,\,V[X]=k\mu ^{2}={\frac {k}{\lambda ^{2}}}}$

他の分布との関係

ガンマ分布との関係

定義より、アーラン分布はガンマ分布で形状母数 k を正の整数に限定したものといえる。また、相型分布の特別な場合でもある。

指数分布の和との関係

アーラン分布は、互いに独立で同一の指数分布に従う確率変数の和を用いて解釈することができる。すなわち、互いに独立でパラメータ λ の指数分布に従う n 個の確率変数 X₁, X₂, …, X_n に対して、その和で表される確率変数${\displaystyle S_{n}=X_{1}+X_{2}+\cdots +X_{n}}$はパラメータ λ, n のアーラン分布に従う。n = 1 の場合は、明らかに指数分布に一致する。

ポアソン分布との関係

S_n をパラメータ λ および n のアーラン分布に従う連続確率変数とし、N(t) をパラメータ λt（ただし t > 0）のポアソン分布に従う離散確率変数とすると、両者の間には

${\displaystyle P(S_{n}\leq t)=P(N(t)\geq n)}$

なる関係が成立する。これはアーラン分布の累積分布関数の形から明らかであるが、指数分布を用いた説明も可能である。すなわち、互いに独立で同一の指数分布に従う時間間隔で生起する事象列を観測するとき、S_n は n 回目の事象が生起した時点であり、N(t) は時点 t までに生起した事象の数を意味する。「n 回目の事象が生起した時点が t 以前である」という事象は、「時点 t までに少なくとも n 回の事象が起きている」という事象と等しいため、この等式が成立する。

関連項目

• 確率分布
• 待ち行列
• ガンマ分布
• ポアソン分布