Không gian tôpô tích

Trong tô pô và các ngành toán học liên quan, không gian tích là tích Descartes của một họ không gian tô pô được trang bị một tôpô gọi là tô pô tích. Tô pô này khác với các loại khác, điển hình là tô pô hộp. Tô pô hộp của một không gian tích trở thành tô pô tích khi nó xác định trên không gian hữu hạn. Tuy vậy, tô pô tích cho phép không gian tích thực hiện được phép tích đối với các nhân tử của nó.^[1][2]

Định nghĩa

Không gian X thỏa mãn^[1]

${\displaystyle X:=\prod _{i\in I}X_{i},}$

là tích Descartes của không gian tô pô ${\displaystyle X_{i}}$, đánh số bởi ${\displaystyle i\in I}$, và phép chiếu ${\displaystyle p_{i}}$: ${\displaystyle X}$ → ${\displaystyle X_{i}}$, tô pô tích trên ${\displaystyle X}$ được định nghĩa là tô pô yếu nhất (hay tô pô có ít tập mở nhất) đối với mọi phép chiếu liên tục ${\displaystyle p_{i}}$. Tô pô tích còn được gọi là tô pô Tychonoff.^[1][3]

• Trường hợp ${\displaystyle X}$ và ${\displaystyle Y}$ là không gian tô pô, thì tô pô tích trên ${\displaystyle X\times Y}$ là tô pô sinh bởi cơ sở ${\displaystyle {\mathcal {B}}=\left\{B\times C\mid B\in {\mathcal {B}}_{X}\wedge C\in {\mathcal {B}}_{Y}\right\}}$ với ${\displaystyle {\mathcal {B}}_{X}}$ là một cơ sở của tô pô ${\displaystyle X}$ và ${\displaystyle {\mathcal {B}}_{Y}}$ là một cơ sở cho tô pô Y

Cho ${\displaystyle p_{X}\,:\,X\times Y\rightarrow X}$ được định nghĩa bởi ${\displaystyle p_{X}(x,\,y)=x}$ và cho ${\displaystyle p_{Y}\,:\,X\times Y\rightarrow Y}$ được định nghĩa bởi ${\displaystyle p_{Y}(x,\,y)=y}$. thì họ ${\displaystyle S=\left\{p_{X}^{-1}(U)\right\}\cup \left\{p_{Y}^{-1}(V)\right\}}$ với ${\displaystyle U}$ mở trong ${\displaystyle X}$ và ${\displaystyle V}$ mở trong ${\displaystyle Y}$ là một cơ sở con của tô pô ${\displaystyle X\times Y}$.

• Trường hợp tích vô hạn

${\displaystyle \{X_{i}\}_{i\in I}}$ là một họ được đánh chỉ số các không gian tô pô, ${\displaystyle X=\prod _{i\in I}X_{i}}$ Định nghĩa tô pô tích trên ${\displaystyle X}$ là tô pô sinh bởi ${\displaystyle S}$. ${\displaystyle \tau _{X}}$ có một cơ sở là ${\displaystyle F=\{\prod _{i\in I}U_{i}\in \tau _{Y},\,U_{i}=X_{i}\,{\text{trừ ra hữu hạn}}\,\ i\in I\}}$ Tô pô tích trên ${\displaystyle \prod _{i\in I}X_{i}}$ có cơ sở là những tập có dạng ${\displaystyle \prod _{i\in I}U_{i}}$ với ${\displaystyle U_{i}}$ mở trong ${\displaystyle X_{i}}$ cho mỗi ${\displaystyle i}$ và ${\displaystyle U_{i}=X_{i}}$ trừ ra hữu hạn giá trị ${\displaystyle i}$.

• Tô pô hộp là tô pô trên ${\displaystyle \prod _{i\in I}X_{i}}$ có cơ sở là những tập có dạng ${\displaystyle \prod _{i\in I}U_{i}}$ với ${\displaystyle U_{i}}$ mở trong ${\displaystyle X_{i}}$ cho mỗi ${\displaystyle i}$.

Ví dụ

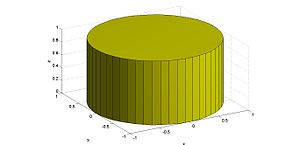
1. Tích Tôpô ${\displaystyle \{x^{2}+y^{2}\leq 1\}\times [0,1]}$ là hình trụ đặc có bán kính đáy 1, chiều cao 1 như hình vẽ.
2. Tôpô trên ${\displaystyle \mathbb {R} ^{2}}$ như là tích các không gian tô pô Euclid của ${\displaystyle \mathbb {R} }$ là tô pô Euclid.^[3]
3. Hình xuyến là một mặt đóng trong ${\displaystyle \mathbb {R} ^{3}}$, nhưng cũng có thể định nghĩa nó là như tích tô pô ${\displaystyle S^{1}\times S^{1}}$ trong đó ${\displaystyle S^{1}}$ là đường tròn (hoặc cung kín) trong ${\displaystyle \mathbb {R} ^{2}}$. Theo cách này có thể coi hình xuyến là không gian tô pô con của ${\displaystyle \mathbb {R} ^{4}}$. Tô pô của ${\displaystyle S^{1}}$ là không gian tô pô con giống như tập con của ${\displaystyle \mathbb {R} ^{2}}$.^[3]
4. Trong ${\displaystyle \mathbb {R^{N}} }$, cho dãy khoảng mở ${\displaystyle (a_{1},\,b_{1}),\,(a_{2},\,b_{2}),\,...}$ trong ${\displaystyle \mathbb {R} }$, tập ${\displaystyle (a_{1},\,b_{1})\times (a_{2},\,b_{2})\times ...}$ là một tập mở cơ sở cho tô pô hộp, chú ý tập này không mở trong tô pô tích.
5. Tập ${\displaystyle (a_{1},\,b_{1})\times (a_{2},\,b_{2})\times ...\mathbb {\times R} \times ...}$ là một tập mở cơ sở của tô pô tích ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$.

Tính Chất

Không gian tích ${\displaystyle X}$, cùng với phép chiếu chuẩn tắc, đặc trưng bởi tính chất phổ quát sau:

• Tô pô tích là tô pô thô nhất trên ${\displaystyle X}$ sao cho tất cả các ánh xạ chiếu ${\displaystyle p_{i}}$ liên tục. Hay nói cách khác, tô pô tích là tô pô sinh bởi những ánh xạ chiếu.
• Nếu ${\displaystyle Y}$ là một không gian tô pô, và đối với mỗi ${\displaystyle i\in I}$, ${\displaystyle f_{i}:\,Y\longrightarrow X_{i}}$ là một ánh xạ liên tục, thì tồn tại một ánh xạ liên tục ${\displaystyle f:\,Y\longrightarrow X}$ sao cho mỗi ${\displaystyle i\in I}$ tuân theo biểu đồ giao hoán:

Nó thể hiện không gian tích là tích phạm trù của các không gian tô pô. Từ tính chất phổ quát trên, ánh xạ ${\displaystyle f:Y\longrightarrow X}$ là liên tục nếu và chỉ nếu ${\displaystyle f_{i}=p_{i}of}$ liên tục cho mọi ${\displaystyle i\in I}$. Trong nhiều trường hợp có thể dễ dàng kiểm tra rằng hàm ${\displaystyle f_{i}}$ là liên tục. Tuy nhiên chứng minh ${\displaystyle g:\,X\longrightarrow Z}$ liên tục thì khó hơn; và cần đến giả thiết ${\displaystyle p_{i}}$ liên tục.

Để thỏa mãn tính liên tục, phép chiếu chuẩn tắc ${\displaystyle p_{i}:\,X\rightarrow X_{i}}$ cần thêm tính chất là những ánh xạ mở. Điều này có nghĩa là bất kỳ tập con mở nào của không gian tích vẫn là mở khi thực hiện chiếu chúng vào ${\displaystyle X_{i}}$. Điều ngược lại không đúng: nếu ${\displaystyle W}$ là không gian con của không gian tích mà phép chiếu vào mọi ${\displaystyle X_{i}}$ là mở, thì ${\displaystyle W}$ không cần thiết là không gian mở trong ${\displaystyle X}$.Các phép chiếu chuẩn tắc nói chung không phải là ánh xạ đóng (ví dụ ${\displaystyle \{(x,y)\in \mathbb {R} ^{2}\mid xy=1\},}$, mà phép chiếu lên hai trục tọa độ là ${\displaystyle \mathbb {R} \setminus \left\{0\right\}}$).

Tô pô tích còn gọi là tô pô hội tụ theo từng điểm bởi vì: một dãy số (hoặc lưới) trong X hội tụ nếu và chỉ nếu mọi phép chiếu của nó vào không gian ${\displaystyle X_{i}}$ hội tụ. Đặc biệt, nếu xét không gian ${\displaystyle X=\mathbb {R^{\mbox{I}}} }$ của mọi hàm giá trị thực trên ${\displaystyle X}$, sự hội tụ trong tô pô tích là giống với sự hội tụ theo điểm của hàm số.

• Ánh xạ vào không gian tích là liên tục khi và chỉ khi tất cả các ánh xạ thành phần là liên tục.
• Tích các tập con đóng bất kỳ ${\displaystyle X_{i}}$ là tập đóng trong ${\displaystyle X}$.

Một định lý quan trọng về tô pô tích là định lý Tychonoff: tích của một họ không gian compact bất kỳ là compact. Định lý này có thể chứng minh dễ dàng cho trường hợp hữu hạn, trong khi trường hợp tổng quát tương đương với tiên đề chọn.^[4]

Liên quan đến khái niệm tôpô khác

• Tiên đề tách
  • Tích của những không gian ${\displaystyle T_{0}}$ thì ${\displaystyle T_{0}}$
  • Tích của những không gian ${\displaystyle T_{1}}$ thì ${\displaystyle T_{1}}$
  • Tích của những không gian Hausdorff thì Hausdorff^[5]
  • Tích của những không gian chính tắc thì chính tắc.
  • Tích của những không gian chuẩn tắc thì không chắc là chuẩn tắc.
• Compắc
  • Tích của những không gian compact thì compact (Định lý Tychonoff)
• Sự liên thông
  • Tích của những không gian liên thông (Liên thông đường) thì liên thông (Liên thông đường)

Chú thích

Tham khảo

• Willard, Stephen (1970). General Topology. Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0486434796. Truy cập ngày 13 tháng 2 năm 2013.

Liên kết ngoài

• “product topology”. PlanetMath.