Wypukłość funkcji

Wypukłość i wklęsłość funkcji – własności funkcji mówiące o położeniu jej wykresu względem stycznej do niego w danym punkcie. Jeśli wykres znajduje się

• nad styczną – mówimy, że jest wypukła,
• pod styczną – mówimy, że jest wklęsła.

Definicja

Wypukłość

Funkcję rzeczywistą ${\displaystyle f}$ określoną na zbiorze wypukłym ${\displaystyle C}$ nazywamy wypukłą, jeżeli

${\displaystyle \forall _{x_{1},x_{2}\in C}\ \forall _{\alpha ,\beta \in [0,1],\,\alpha +\beta =1}\ f(\alpha x_{1}+\beta x_{2})\leqslant \alpha f(x_{1})+\beta f(x_{2}).}$

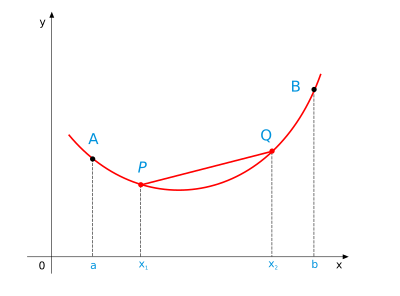
Jeśli ${\displaystyle C}$ jest przedziałem, to geometryczny sens powyższej nierówności jest następujący: łuk wykresu funkcji łączący dowolne dwa punkty ${\displaystyle P,Q}$ tego wykresu leży poniżej lub na cięciwie ${\displaystyle PQ}$^[1].

Wklęsłość

Funkcję ${\displaystyle f\colon C\to \mathbb {R} }$ nazywamy wklęsłą w tym przedziale, jeżeli w powyższej definicji słowo poniżej zastąpimy przez powyżej, czyli innymi słowy zmienimy zwrot nierówności. Jeszcze inaczej: funkcja ${\displaystyle f}$ jest wklęsła, jeśli funkcja ${\displaystyle -f}$ jest wypukła.

Terminologia

Niewielka liczba autorów nazywa funkcje wypukłe w sensie powyższej definicji wklęsłymi i na odwrót; spotyka się też określenia wypukła w dół i wypukła w górę na funkcje wypukłą i wklęsłą odpowiednio.

Zastępując nierówności w definicji wypukłości (wklęsłości) przez nierówności ostre definiujemy funkcje ściśle wypukłe (ściśle wklęsłe)

Własności

Można pokazać, że funkcja wypukła – a zatem i wklęsła – na zbiorze otwartym jest ciągła^{[potrzebny przypis]}. Założenie to jest istotne.

Funkcja wypukła jest kresem górnym rodziny funkcji liniowych mniejszych bądź równych od niej (punktowo).

Kryterium wypukłości funkcji ciągłych

Jeśli funkcja ${\displaystyle f}$ jest funkcją ciągłą określoną na przedziale ${\displaystyle P\subset \mathbb {R} }$ spełnia warunek

${\displaystyle \forall _{x,y\in P}\;f\left({\frac {x}{2}}+{\frac {y}{2}}\right)\leqslant {\frac {f(x)+f(y)}{2}}}$

to funkcja jest wypukła na tym przedziale. Prawdziwa jest również implikacja odwrotna^{[potrzebny przypis]}.

Funkcja różniczkowalna

Jeśli funkcja ${\displaystyle f}$ jest funkcją różniczkowalną określoną na przedziale otwartym, można podać równoważne definicje opierające się na pojęciu stycznej.

Wypukłość

Funkcja ${\displaystyle f(x)}$ jest wypukła w przedziale ${\displaystyle (a,b)}$ wtedy i tylko wtedy, gdy wykres funkcji leży ponad wykresem stycznej dla każdego punktu ${\displaystyle x_{0}}$ z przedziału ${\displaystyle (a,b).}$ W przypadku funkcji różniczkowalnej zapisuje się to wzorem

${\displaystyle \forall _{x,x_{0}\in (a,b)}\;f(x)-f(x_{0})\geqslant f'(x_{0})(x-x_{0}).}$

Równanie stycznej do krzywej ${\displaystyle y=f(x)}$ w punkcie ${\displaystyle x_{0}}$ ma postać: ${\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}$

Jeśli funkcja ${\displaystyle f(x)}$ jest dwukrotnie różniczkowalna na ${\displaystyle (a,b),}$ to aby była ona wypukła (wklęsła ku dołowi) w przedziale ${\displaystyle (a,b),}$ wystarczy żeby jej druga pochodna w tym przedziale była nieujemna: ${\displaystyle \forall _{x\in (a,b)}\;f''(x)\geqslant 0.}$

Wklęsłość

Funkcja ${\displaystyle f(x)}$ jest wklęsła w przedziale ${\displaystyle (a,b)}$ wtedy i tylko wtedy, gdy wykres funkcji leży pod wykresem stycznej dla każdego punktu ${\displaystyle x_{0}}$ z przedziału ${\displaystyle (a,b).}$ W przypadku funkcji różniczkowalnej zapisuje się to wzorem:

${\displaystyle \forall _{x,x_{0}\in (a,b)}\;f(x)-f(x_{0})\leqslant f'(x_{0})(x-x_{0}).}$

Jeśli funkcja ${\displaystyle f(x)}$ jest dwukrotnie różniczkowalna na ${\displaystyle (a,b),}$ to aby była ona wklęsła (wypukła ku górze) (w przedziale ${\displaystyle (a,b)}$), wystarczy żeby druga pochodna w tym przedziale była niedodatnia^[2]: ${\displaystyle \forall _{x\in (a,b)}f''(x)\leqslant 0.}$

Punkt przegięcia

 Główny artykuł: Punkt przegięcia.

Jeżeli z jednej strony punktu ${\displaystyle x_{0}}$ funkcja jest wypukła zaś z drugiej wklęsła, to ${\displaystyle x_{0}}$ nazywamy punktem przegięcia krzywej.

O ile druga pochodna w punkcie ${\displaystyle x_{0}}$ istnieje, warunkiem koniecznym na to aby punkt ${\displaystyle x_{0}}$ był punktem przegięcia funkcji ${\displaystyle f}$ jest:

${\displaystyle f''(x_{0})=0.}$

Nie jest to jednak warunek wystarczający, gdyż w punkcie ${\displaystyle x_{0}}$ musi nastąpić zmiana znaku drugiej pochodnej.

Przykład

Rozważmy funkcję rzeczywistą ${\displaystyle f(x)=x^{4}.}$ Jej druga pochodna ${\displaystyle f''(x)=12x^{2}}$ zeruje się jedynie w punkcie ${\displaystyle x_{0}=0.}$ W tym punkcie nie następuje jednak zmiana znaku drugiej pochodnej co oznacza, że funkcja ${\displaystyle f}$ nie ma punktów przegięcia. Ponadto druga pochodna jest nieujemna w całej dziedzinie, więc funkcja ${\displaystyle f}$ jest funkcją wypukłą w całej dziedzinie.

Zobacz też

• nierówność Jensena

Przypisy