Rozkład logistyczny

Rozkład logistyczny

Gęstość prawdopodobieństwa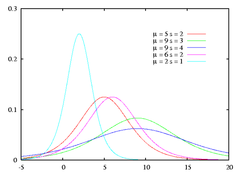
Dystrybuanta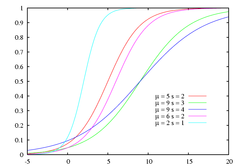
Parametry	${\displaystyle \mu }$ parametr położenia (liczba rzeczywista) ${\displaystyle s>0}$ parametr skali (liczba rzeczywista)
Nośnik	${\displaystyle x\in (-\infty ;+\infty )}$
Gęstość prawdopodobieństwa	${\displaystyle {\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}}$
Dystrybuanta	${\displaystyle {\frac {1}{1+e^{-(x-\mu )/s}}}}$
Wartość oczekiwana (średnia)	${\displaystyle \mu }$
Mediana	${\displaystyle \mu }$
Moda	${\displaystyle \mu }$
Wariancja	${\displaystyle {\frac {\pi ^{2}}{3}}s^{2}}$
Współczynnik skośności	${\displaystyle 0}$
Kurtoza	${\displaystyle 6/5}$
Entropia	${\displaystyle \ln(s)+2}$
Funkcja tworząca momenty	${\displaystyle e^{\mu \,t}\,\mathrm {B} (1-s\,t,\;1+s\,t)}$ dla ${\displaystyle |s\,t|<1,}$ funkcja beta
Funkcja charakterystyczna	${\displaystyle e^{i\mu t}\,\mathrm {B} (1-ist,\;1+ist)}$ dla ${\displaystyle |ist|<1}$

Rozkład logistyczny – ciągły rozkład prawdopodobieństwa używany w szczególności do opisu analitycznego procesów wzrostu osiągających stan wysycenia.

Rozkład logistyczny ma jako podstawę funkcję logistyczną^[1]:

${\displaystyle l(x)={\frac {g}{1+d\cdot e^{-cx}}},}$

${\displaystyle g}$ wyznacza przy tym granicę wysycenia. Normalizując funkcję logistyczną przez podstawienie ${\displaystyle g\equiv 1,}$ uzyskujemy funkcję opisującą rozkład logistyczny. Zazwyczaj stosuje się dalsze podstawienia:

${\displaystyle e^{\tfrac {\mu }{s}}=d}$

oraz

${\displaystyle {\tfrac {1}{s}}=c.}$

Symetria

Logistyczna zmienna losowa jest symetryczna względem wartości oczekiwanej ${\displaystyle \alpha ,}$ który jest jednocześnie medianą rozkładu.

Kwantyle

Do obliczenia kwantyli można użyć funkcji odwrotnej:

${\displaystyle F^{-1}(p)=\mu -s\ln \left({\frac {1-p}{p}}\right).}$

Zastosowanie

Przy pomocy rozkładu logistycznego opisuje się w statystyce czas trwania jakiegoś stanu, np. trwałość urządzeń elektronicznych. Dalej używa się rozkładu również do estymacji wskaźnika struktury dychotomicznej zmiennej w tzw. regresji Logit. Często stosuje się w statystyce wszakże również funkcję logistyczną, np. w nieliniowej metodzie najmniejsczych kwadratów do estymacji szeregów czasowych.

Przykład

Na podstawie długoletniego doświadczenia wiadomo, że czas niezawodnego działania elektrycznych szczoteczek do zębów pewnego producenta opisuje dobrze rozkład logistyczny z wartością oczekiwaną 8 lat i wariancją σ² = 4 lata². Można więc zapisać

${\displaystyle \mu =8}$ oraz

${\displaystyle s={\frac {\sigma \cdot {\sqrt {3}}}{\pi }}={\frac {2\cdot {\sqrt {3}}}{\pi }}\approx 1{,}10.}$

Tak na przykład prawdopodobieństwo, że szczoteczka do zębów będzie działać przez ponad dziesięć lat wynosi:

${\displaystyle \mathrm {P} (X>10)=1-\mathrm {P} (X\leqslant 10)=1-{\frac {1}{1+e^{-{\frac {10-8}{1,1}}}}}=1-0{,}8538=0{,}1462.}$

A więc ok. 15% wszystkich szczoteczek będzie działać co najmniej dziesięć lat.

Poszukajmy teraz okresu, po jakim 99,95% wszystkich szczoteczek działa niezawodnie.

${\displaystyle F^{-1}(0{,}9995)\approx 8-1{,}10\ln {\frac {0{,}9995}{1-0{,}9995}}\approx -0{,}36044.}$

Odpowiedź jest absurdalna: ok. 4 miesięcy przed wyprodukowaniem. W tym przykładzie przyjęto, że czas niezawodnego działania szczoteczek do zębów w szerokim zakresie (ale nie w całym ${\displaystyle \mathbb {R} }$) jest dobrze opisywany przez teoretyczny rozkład (logistyczny) zmiennej losowej.

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Logistic Distribution, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-08-30].
• Logistic distribution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-08-30].