Normale verdeling

Normale verdeling
Kansdichtheid  standaardnormale verdeling
Verdelingsfunctie Kleuren komen overeen met de kansdichtheden hierboven
Parameters	${\displaystyle \mu }$ locatie (reëel) ${\displaystyle \sigma ^{2}>0}$ gekwadrateerde schaal (reëel)
Drager	${\displaystyle x\in (-\infty ;+\infty )}$
Kansdichtheid	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi \ }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$
Verdelingsfunctie	${\displaystyle {\frac {1}{2}}\left(1+\mathrm {erf} \ {\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)}$
Verwachtingswaarde	${\displaystyle \mu }$
Mediaan	${\displaystyle \mu }$
Modus	${\displaystyle \mu }$
Variantie	${\displaystyle \sigma ^{2}}$
Scheefheid	0
Kurtosis	0
Entropie	${\displaystyle \ln \left(\sigma {\sqrt {2\ \pi \ e\ }}\right)}$
Moment- genererende functie	${\displaystyle M_{X}(t)=\exp \left(\mu \ t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}$
Karakteristieke functie	${\displaystyle \varphi _{X}(t)=\exp \left(\mu \ i\ t-{\frac {\sigma ^{2}t^{2}}{2}}\right)}$
Portaal    Wiskunde

De normale verdeling of gaussverdeling, genoemd naar de Duitse wiskundige Carl Friedrich Gauss, is een continue kansverdeling met twee parameters, de verwachtingswaarde ${\displaystyle \mu }$ en de standaardafwijking ${\displaystyle \sigma }$, waarvan de kansdichtheid wordt gegeven door de volgende Gaussische functie:

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi \ }}}}\ e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}$

De kansdichtheid is symmetrisch rond ${\displaystyle \mu }$, hoog in het midden, en wordt naar lage en hoge waarden steeds kleiner zonder ooit echt nul te worden. Door de vorm wordt deze ook wel klokkromme of gausscurve genoemd.

De normale verdeling wordt wel genoteerd als ${\displaystyle N(\mu ,\sigma ^{2})}$-verdeling, wat wil zeggen dat het een normale verdeling is met verwachtingswaarde ${\displaystyle \mu }$ en variantie ${\displaystyle \sigma ^{2}}$.

Zoals voor elke kansdichtheid is de integraal over het hele definitiegebied precies gelijk aan 1:

${\displaystyle \int \limits _{-\infty }^{+\infty }{\frac {1}{\sigma {\sqrt {2\pi \ }}}}\ e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}{\rm {d}}x=1}$

Veel verschijnselen zijn benaderend te beschrijven met behulp van een normale verdeling. Het gaat dan om verschijnselen waarvan de verdeling symmetrisch geconcentreerd is rond een centrale waarde en afwijkingen van deze centrale waarde steeds onwaarschijnlijker worden naarmate de afwijking groter is. Soms is het verschijnsel de optelsom van een groot aantal effecten die elkaar niet beïnvloeden. De centrale limietstelling geeft in zo'n geval de voorwaarden waaronder het totaal normaal verdeeld zal zijn. De normale verdeling is niet altijd een goede benadering. Zo zijn andere verdelingen beter als er sprake is van exponentiële groei, zoals het geval is bij onder meer inkomen, prijzen en bevolkingsomvang waarbij er een scheefheid naar rechts is. Verdelingen als de lognormale verdeling of de paretoverdeling kunnen dan een betere benadering geven.

Standaardnormale verdeling

Een normale verdeling met verwachtingswaarde 0 en variantie 1, de ${\displaystyle N(0,1)}$-verdeling, wordt een standaardnormale verdeling genoemd. De bijbehorende dichtheid is:

${\displaystyle \varphi (x)={\frac {1}{\sqrt {2\pi \ }}}\ e^{-{\frac {1}{2}}x^{2}}}$

Zie ook: z-scores.

Eigenschappen

Lineaire transformatie

Als de toevalsvariabele ${\displaystyle X}$ ${\displaystyle N(\mu ,\sigma ^{2})}$-verdeeld is, geldt voor willekeurige ${\displaystyle a}$ en ${\displaystyle b}$:

${\displaystyle aX+b\sim N\left(a\mu +b,\,a^{2}\sigma ^{2}\right)}$

Een specifiek resultaat van deze eigenschap is dat

${\displaystyle Z={\frac {X-\mu }{\sigma }}\sim N(0,1)}$,

dus standaardnormaal verdeeld is.

Lineaire combinatie

Zijn twee toevalsvariabelen ${\displaystyle X}$ en ${\displaystyle Y}$ normaal verdeeld en ongecorreleerd met respectievelijke parameters ${\displaystyle \mu _{X}}$ en ${\displaystyle \sigma _{X}^{2}}$ en ${\displaystyle \mu _{Y}}$ en ${\displaystyle \sigma _{Y}^{2}}$, dan geldt:

${\displaystyle X+Y\sim N(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$

${\displaystyle X-Y\sim N(\mu _{X}-\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$

In het algemeen geldt voor ongecorreleerde normaal verdeelde variabelen ${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$, met ${\displaystyle \mathrm {E} X_{i}=\mu _{i}}$ en ${\displaystyle \mathrm {var} (X_{i})=\sigma _{i}^{2}}$, dat elke lineaire combinatie hiervan ook normaal verdeeld is.

Voor willekeurige reële getallen ${\displaystyle a_{1},a_{2},\ldots ,a_{n}}$ geldt dat

${\displaystyle \sum _{i=1}^{n}a_{i}X_{i}\sim N\left(\sum _{i=1}^{n}a_{i}\mu _{i},\sum _{i=1}^{n}(a_{i}\sigma _{i})^{2}\right)}$

Vuistregel

Binnen een afstand van één standaardafwijking van de verwachtingswaarde ligt ongeveer 68% van het oppervlak onder de grafiek van de kansdichtheid van de normale verdeling, ongeveer 95% binnen twee standaardafwijkingen afstand van de verwachtingswaarde. De curve gaat daarna vrij snel naar nul: ongeveer 99,99% van het oppervlak ligt binnen vier standaardafwijkingen afstand van het midden. Afwijkingen van meer dan vier standaardafwijkingen van het midden zijn dus zeer zeldzaam.

Voorkomen

Voor veel natuurlijk voorkomende verschijnselen is een normale verdeling een goede benadering van de frequentie waarmee bepaalde meetwaarden kunnen voorkomen; daarom wordt vaak een normale verdeling verondersteld voor de onderliggende (populatie)verdeling. De parameters ${\displaystyle \mu }$ en ${\displaystyle \sigma ^{2}}$ van deze normale verdeling kunnen dan benaderd worden (geschat) met respectievelijk het steekproefgemiddelde ${\displaystyle {\bar {x}}}$ en de steekproefvariantie ${\displaystyle s^{2}}$. Zo kan men een schatting maken van de gemiddelde lengte van Nederlandse mannen en de standaardafwijking van de verdeling door een steekproef van een honderdtal mannen te nemen en daarvan de lengte te meten. De wiskunde vertelt ook hoe nauwkeurig in zo'n geval ${\displaystyle {\bar {x}}}$ een benadering is voor ${\displaystyle \mu }$, en hoe nauwkeurig ${\displaystyle s^{2}}$ een benadering is voor ${\displaystyle \sigma ^{2}}$.

Het was Adolphe Quetelet die voor het eerst het verband zag tussen de normale verdeling en natuurkundige verschijnselen. Hij vond deze relatie tijdens zijn onderzoek naar een wiskundige formule om de gezondheid van de soldaten te bepalen. Deze relatie is intussen bekend als de Queteletindex, en ook als de body mass index BMI. Quetelet was een leerling van Gauss en na zijn bezoek in Göttingen onderhielden zij een correspondentie, die nog altijd bewaard is gebleven.

Andere voorbeelden van grootheden die als normaal verdeeld beschouwd kunnen worden, zijn:

• de maximumtemperatuur op 5 augustus in De Bilt, gemeten over verschillende jaren
• de afwijking van klokken van één bepaald merk in seconden per dag
• de intelligentie van een grote groep proefpersonen van dezelfde leeftijd

Bij medische laboratoriumtests wordt dikwijls aangenomen dat de bij gezonde proefpersonen gevonden waarden een normale verdeling vertonen. De waarden binnen een afstand van twee keer de standaardafwijking van het midden worden dan "normaal" genoemd. Volgens deze definitie wordt bij 5% van de gezonde mensen een abnormale waarde gevonden.

Normale benadering

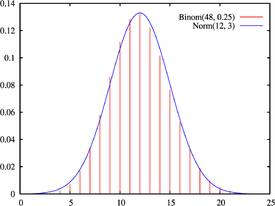
In een groot aantal gevallen kan een verdeling benaderd worden door een geschikt gekozen normale verdeling. In het bijzonder in die gevallen waarin de centrale limietstelling van praktische toepassing is. Zo kan een binomiale verdeling met parameters ${\displaystyle n}$ en ${\displaystyle p}$, voor grotere waarden van ${\displaystyle n}$ en gemiddelde waarden voor ${\displaystyle p}$, benaderd worden door een normale verdeling met dezelfde verwachting en variantie als de binomiale, dus door een ${\displaystyle N(np,np(1-p))}$-verdeling. In de figuur is dit geschetst voor ${\displaystyle n=48}$ en ${\displaystyle p=0{,}25}$. Als ${\displaystyle X}$ een stochastische variabele is met de genoemde binomiale verdeling, kunnen we ${\displaystyle X}$ praktisch als ${\displaystyle N(12,9)}$-verdeeld beschouwen. Dan is:

${\displaystyle P(X\leq 15)\approx P(Y\leq 15)=P(Z\leq {\tfrac {15-12}{3}})=\Phi (1)=0{,}8415}$.

Hierin is ${\displaystyle Y}$ ${\displaystyle N(12,9)}$-verdeeld, ${\displaystyle Z}$ standaardnormaal en ${\displaystyle \Phi }$ de standaardnormale verdelingsfunctie.

Continuïteitscorrectie

De benadering is beter als de zogenaamde continuïteitscorrectie wordt toegepast. Deze berust op de vaststelling dat ${\displaystyle P(X\leq 15)=P(X<16)}$, maar de bijbehorende benaderingen ${\displaystyle P(Y\leq 15)}$ en ${\displaystyle P(Y<16)}$ enigszins verschillen. Als betere benadering neemt men: ${\displaystyle P(Y\leq 15+{\tfrac {1}{2}})}$.

Bivariate normale verdeling

De eendimensionale normale verdeling heeft equivalenten in meer dimensies; deze worden multivariate normale verdelingen genoemd. De bivariate (dat wil zeggen tweedimensionale) normale verdeling wordt bepaald door vijf parameters: ${\displaystyle \mu ,\sigma ^{2},\nu ,\tau ^{2}}$ en ${\displaystyle \rho }$, die respectievelijk de verwachting en variantie in de eerste en tweede dimensie en de correlatiecoëfficiënt tussen beide dimensies voorstellen. Men noteert hiervoor wel: ${\displaystyle N(\mu ,\sigma ^{2},\nu ,\tau ^{2},\rho )}$-verdeling. De kansdichtheid is:

${\displaystyle f(x,y)={\frac {1}{2\pi \sigma \tau {\sqrt {1-\rho ^{2}\ }}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left(\left({x-\mu \over \sigma }\right)^{2}-2\rho \left({x-\mu \over \sigma }\right)\left({y-\nu \over \tau }\right)+\left({y-\nu \over \tau }\right)^{2}\right)\right)}$

De structuur van de formule is beter te zien voor de ${\displaystyle N(0,1,0,1,\rho )}$-verdeling. Dan is de kansdichtheid:

${\displaystyle f(x,y)={\frac {1}{2\pi {\sqrt {1-\rho ^{2}\ }}}}\exp \left(-{x^{2}-2\rho xy+y^{2} \over 2(1-\rho ^{2})}\right)}$

Zie ook multivariate normale verdeling.

Zie ook

• Normaal waarschijnlijkheidspapier

Andere verdelingen

• De normale verdeling is geen goede beschrijving voor een populatie die is opgebouwd uit verschillende subpopulaties, waardoor soms een meertoppige verdeling ontstaat.
• Ook is de normale verdeling geen goede beschrijving voor verdelingen waarbij een klein aantal heel grote afwijkingen mogelijk is. Men spreekt dan van 'dikke staarten'. In dat geval kan soms de t-verdeling gebruikt worden.
• Als de toevariabele ${\displaystyle X}$ normaal verdeeld is, heeft ${\displaystyle Y=e^{X}}$ een lognormale verdeling.

Websites

• Online Calculator Normale verdeling

Zie de categorie Normal distribution van Wikimedia Commons voor mediabestanden over dit onderwerp.