Associativiteit (wiskunde)

In de wiskunde is associativiteit een eigenschap van een binaire operatie. Het betekent dat, als de associatieve operator twee of meer keer achter elkaar voorkomt, de bewerkingsvolgorde niet van belang is, onder de voorwaarde dat de volgorde van de operanden niet verandert. Dat betekent in de praktijk dat het verplaatsen van haakjes in een uitdrukking de uitkomst van de uitdrukking niet verandert.

Definitie

Een binaire operatie ${\displaystyle *}$ op een verzameling ${\displaystyle S}$ wordt associatief genoemd, indien voor alle ${\displaystyle x,y,z\in S}$ geldt:

${\displaystyle (x*y)*z=x*(y*z)\qquad {\mbox{voor alle }}x,y,z\in S}$

De volgorde waarin de beide operaties worden uitgevoerd, heeft dus geen effect op de uitkomst. Vervolgens kan worden aangetoond dat dit ook geldt voor expressies met daarin ieder aantal operaties ${\displaystyle *}$. Dus wanneer ${\displaystyle *}$ associatief is, kan de evaluatie-volgorde ongespecificeerd blijven, zonder dat dit tot dubbelzinnigheid leidt. De haakjes kunnen daarom worden weggelaten:

${\displaystyle x*y*z}$

Het veranderen van de volgorde van uitvoering van de bewerkingen moet niet worden verward met het van plaats verwisselen van de operanden van een operatie.

Voorbeelden

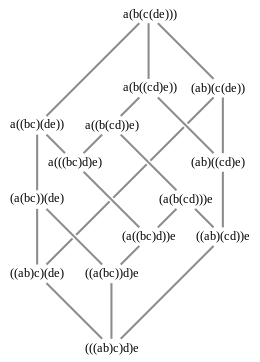
• Beschouw nu twee voorbeelden van binaire associatieve operaties: het optellen en het vermenigvuldigen van natuurlijke getallen.

${\displaystyle a+(b+c)=(a+b)+c}$;

Zo is (5 + 2) + 3 = 7 + 3 = 10 en 5 + (2 + 3) = 5 + 5 = 10.

${\displaystyle a\times (b\times c)=(a\times b)\times c}$;

en (5 × 2) × 3 = 10 × 3 = 30 en 5 × (2 × 3) = 5 × 6 = 30

Optellen en vermenigvuldigen van natuurlijke getallen zijn beide associatieve bewerkingen.

• Optellen en vermenigvuldigen van reële en complexe getallen, het optellen van vectoren en de functiecompositie zijn ook associatief.

• Commutativiteit en distributiviteit zijn overeenkomstige eigenschappen, die aan een bewerking tussen de elementen uit een gegeven verzameling kunnen worden gesteld. Deze eigenschappen worden gebruikt in de definitie van bijvoorbeeld groepen en van lichamen/velden.

• Aftrekken is een voorbeeld van een niet-associatieve bewerking: 5 – (3 – 2) is iets anders dan (5 – 3) – 2.

• Wanneer vijf elementen ${\displaystyle a,b,c,d}$ en ${\displaystyle e}$ in die volgorde met elkaar worden vermenigvuldigd, waarbij de vermenigvuldiging associatief is, geeft dat op 14 verschillende manieren dezelfde uitkomst. De 14 mogelijkheden kunnen in een hasse-diagram worden geïllustreerd. Deze 14 uitkomsten kunnen voor het geval de vermenigvuldiging niet associatief is onderling verschillen.