操作変数法

操作変数法(そうさへんすうほう、英: method of instrumental variables, IV)とは、統計学、計量経済学、疫学、また関連分野において、統制された実験が出来ない時、もしくは処置がランダムに割り当てられない時に、因果関係を推定するための方法である[1]。直感的に言えば、操作変数は説明変数と被説明変数の間の相関が二変数間の因果関係をもっともらしく反映していない時に用いられる。妥当な操作変数は説明変数に影響を与えるが被説明変数に独立的な影響を持たず、研究者が被説明変数に対する説明変数の因果効果を明らかにすることを可能とする。
操作変数法は説明変数(共変数)が回帰モデルにおける誤差項と相関している時に一致推定(英語版)することを可能とする。このような相関は、被説明変数の変化が共変数の少なくとも一つの値を変化させる時("逆"の因果)、説明変数と被説明変数の双方に影響を与える除外変数が存在する時、共変数に測定誤差がある時(error-in-variables models)に起こるだろう。回帰の文脈において一つないしは複数の問題を持つ説明変数は時折、内生性として言及される。この状況下では、最小二乗法はバイアスを持ち一致性を持たない推定量を生み出す[2]。しかし、もし操作変数が利用可能ならば、一致推定量を得ることができる。操作変数とはそれ自身は説明すべき方程式には依存していないが、内生的な説明変数とほかの共変数の値による条件の下で相関している変数のことである。線形モデルにおいては操作変数法を用いるために二つの必要な仮定がある。
- 操作変数は他の共変数で条件付けた時に、内生的な説明変数と相関しなくてはならない。もしこの相関が統計的に有意なほど高ければ、その操作変数は強い第一段階(英: strong first stage)を持つと言う。相関が弱いとパラメータの推定値と標準誤差について間違った推論を導きかねない[3]。
- 操作変数は説明方程式の誤差項と他の共変数で条件付けた時に相関してはならない。言い換えると、操作変数は元の予測変数と同じ問題に直面することがない。もしこの条件が満たされているならば、その操作変数は除外制約(英: exclusion restriction)を満たすと言う。
導入
操作変数法の概念はフィリップ・ライト(英: Philip G. Wright)と共著者で息子のシューアル・ライトにより、1928年に出版された著書The Tariff on Animal and Vegetable Oils[4][5]において同時方程式(英語版)の文脈で導出された。1945年、Olav Reiersøl は彼の学位論文において、errors-in-variables modelsの文脈で同じ手法を用い、その手法に名前を与えた[6]。
操作変数法の背後にあるアイデアは広いモデルのクラスに拡張できるが、操作変数法についての非常に一般的な文脈は線形回帰にある。伝統的に、操作変数は で定義され、操作変数と相関を持つ独立変数は 、操作変数と無相関な誤差項は として定義され、以下のような方程式を満たす[7]。
ここで は通常、1のみからなる列と他の共変数からなる追加的な列を持つ行列である。この場合において操作変数が解くことのできる問題について考えよう。すると、操作変数法がいかにして問題を解くかを示すことができる。最小二乗法(OLS)が、 の下で について問題を解くことを思い出そう(これは簡単である。誤差の二乗和を最小化する時、、一階条件はまさしく である)。もし、上でリストアップした理由の一つのために、本当のモデルでは であるとしたら、例えばもし と の両方に別々に影響を与える除外変数が存在するならば、OLSの手続きは、 に対する の因果的な効果を生み出さないだろう。OLSはただ単純に と相関しないように結果的になる誤差を生み出すパラメータを取り出すであろう。
一変数の場合を用いるとより明確になる。一変数と定数についての回帰を考えているとしよう(ひょっとしたら他の共変数は必要ないかもしれない、またひょっとしたらすでに他の関連する共変数を統制(英語版)しているかもしれない)。
この場合、興味のある説明変数に対する係数は として与えられる[8]。 について代入すると以下のようになる。
もし想定しているモデル上において ならば、OLSは興味のある因果効果を反映していない係数を推定する。操作変数法は、 が と無相関か否かというより、他の変数 が と無相関か否かに基づいてパラメータ を識別するので問題を解決することが可能になる。もし理論上 が と関係し(第一段階)、 と無相関(除外制約)ならば、操作変数法は最小二乗法が失敗した興味のある因果パラメータを識別するだろう。線形の場合には操作変数推定量を使い導出する複数の特定の方法が存在するので、さらなる議論は推定の節で行う。
もちろん、操作変数法はより広い非線形モデルのクラスにも適用されてきた。操作変数の一般的な定義は、反事実的かつグラフィカルな形式論を用いることで、ジューディア・パールによって与えられた[9]。グラフィカルな操作変数の定義は Z が次の条件を満たすことで与えられる。
ここで はベイジアン・ネットワークにおけるd分離(英語版) であり、 は に入る矢印がすべてカットオフされるようなベイジアン・ネットワークにおけるグラフである。
操作変数の反事実的(英: counterfactual)な定義は操作変数 Z が以下を満たすことである。
ここで は が であった時の の取りうる値であり、 は独立を表している。
もし追加的な共変数 があるのならば、 で条件付けた下での操作変数 として定義が変更される。
パールの定義のエッセンスは
- 興味のある方程式は"構造的"なものであり、単なる"回帰"ではない。
- 誤差項 は が定数である時に に影響を与えるすべての外生的要因を表している。
- 操作変数 は と独立でなければならない。
- 操作変数 は が定数ならば、 に影響を与えてはならない。(除外制約)
- 操作変数 は と独立ではない。
ということである。
これらの条件は方程式の特定の関数形に依存しておらず、ゆえに非線形方程式、つまり誤差項 が非加法的である場合にも適用できる。これらの条件はまた複数の方程式からなるシステムにも適用でき、そこでは (と他の要因)がいくつかの中間的な変数を通して に影響を与える。操作変数は の原因である必要はない。そのような原因の代理変数は、条件1から5を満たすならば、操作変数としてまた使えるだろう[9]。また、除外制約(条件4)は条件2と3から導けるので省略できる。
例
カジュアルな言い方では、ある変数 が他の変数 に与える因果効果を推定しようとする時、操作変数は における効果のみを通して に影響を与える変数 のことである。例えば、研究者は喫煙の一般的な健康における因果効果を推定したいとしよう[10]。健康と喫煙の相関は、他の変数が健康と喫煙の両方に影響を与えた、もしくは健康状態が喫煙に影響を与えたと考えることもできるので、喫煙が健康を悪化させる原因であるということは意味しない。一般の母集団において喫煙状態を制御した実験を行うのはとても難しく費用がかかる。研究者は、因果分析における喫煙の操作変数としてタバコ製品の税率の時系列を用いて観測データから健康における喫煙の因果効果を推定しようとするだろう。研究者はタバコ製品についての税率は喫煙に与える効果のみを通して健康に影響を与えると仮定するので、タバコ製品についての税率は操作変数としては合理的な選択である。もし研究者がタバコ税と健康状態が相関しているのを発見できたならば、それは喫煙が健康状態の変化の原因であるという証拠と見なしうる。
ヨシュア・アングリストとアラン・クルーガーは操作変数法の使用と歴史についてのサーベイを行っている[11]。
適切な操作変数の選択
は観測できないので、 が から独立であるという仮定が満たされるかどうかはデータからは導かれず、かわりにモデルの構造、つまりデータの生成過程を決定しなくてはならない。因果のグラフはこの構造を表現していて、上で与えられているグラフの定義は変数 が共変数 が与えられた下で操作変数として機能するかどうかを手早く決めるために用いることが出来る。この点を見るために、以下の例を考えよう。

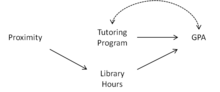


ランダムに学生が寮に割り当てられるような大学において、大学のチュータープログラム(Tutoring Program)がGPAに与える影響を推定したいとしよう。チュータープログラムへの出席とGPAの間の関係は数多くの要因によって混同される。チュータープログラムに出席した学生は自分の成績に注意を払うかもしれないし、努力をするかもしれない(この混同は図.1-3における右側のチュータープログラムとGPAの間の双方向に伸びる弧を通して描写される)。学生が寮にランダムに割り当てられたとして、チュータープログラムが行われる場所からの学生の寮の近さは操作変数の自然な候補になる。
しかしながら、チュータープログラムが大学の図書館で行われたらどうなるだろうか。チュータープログラムが行われる場所と寮の近さは学生がより図書館で時間を費やそうとする原因になりうるだろうし、今度はそれがGPAを改善するだろう(図1を参照)。図2において描写されている因果グラフを用いると、チュータープログラムの行われる場所の近さは、グラフ において「場所の近さ(Proximity) 図書館の使用時間(Library Hours) GPA」という経路を通してGPAと繋がっているため、操作変数としてはふさわしくない。しかしながら、共変数として図書館の使用時間を加えてコントロールすれば、 において図書館の使用時間が与えられた下で場所の近さはGPAから分離されるため、場所の近さは操作変数になる。
今、図3のように学生"そのものが持つ能力"(Ability)が学生のGPAと同じくらい学生の図書館にいる時間に影響を与えるとしよう。因果グラフを用いれば、図書館の使用時間はコライダーとなり、図書館で条件付けることは「場所の近さ(Proximity) 図書館の使用時間(Library Hours) GPA」という経路を作るだろう。結果として、場所の近さは操作変数として用いることは出来ない。
最後に、図4で示されているように、図書館で勉強しない学生は単に他の場所で勉強するので、図書館の使用時間はGPAに何の影響も与えないとしよう。この場合、図書館の使用時間を制御することは場所の近さからGPAまでの信用できない経路を開く。しかしながら、図書館の使用時間をコントロールせず、共変数から除外すると、場所の近さは操作変数として用いることが出来る。
推定
今またここで操作変数法の詳細を考えよう。以下のような形でデータが生成されるとする。
ここで
- は観測値の添え字、
- は被説明変数、
- は説明変数と定数のベクトル、
- は とは異なる に影響を与えるすべての要因を表す観測できない誤差項、
- は観測できないスカラー値のパラメータ、
- 上付きの添え字 は行列ないしはベクトルの転置、
とする。
パラメータ は の各要素が一単位動き、他の に変動を与えるすべての要因が一定である時に が受ける因果効果を表している。計量経済学的な目的は を推定することである。単純化のために、 は互いに無相関で、同じ分散である分布から生成されるものとする。つまり誤差項は自己相関がなく分散均一である。
また同じ形の回帰モデルも導出できるとする。観測値のランダムなサンプルのサイズを とすると、最小二乗法による推定量は以下のようになる。
ここで はそれぞれの を並べた 行の行列、 と は長さ の列ベクトルを表している。この方程式は導入節における についての方程式と類似している(ここでの方程式は行列バージョンである)。 と が無相関であるとき、ある正則条件の下で第2項を で条件付けた期待値は0となり、さらに極限において0に収束する。よってこの推定量は不偏かつ一致推定量である。 と に含まれる測定されない因果変数が相関すると、しかしながら、最小二乗法による推定量は一般的に についてバイアスを持ち、一致性もない。この場合、 の値が与えられた場合の の値を予測するための推定量としては妥当であるが、 の に対する因果効果はこの推定量では分からない。
パラメータ を正しく推定するために、それぞれの内生的な と強く相関するが、 とは相関しない(言い換えれば、 とは相関しない)変数 を導入する。簡単化のために、 は 定数と内生変数の列からなる 行2列の行列であるとし、 は 定数と操作変数の列からなる 行2列の行列であるとする。しかしながら、この方法は が定数と、例えば、5つの内生変数からなる行列であり、 が定数と5つの操作変数からなる場合といった時にも拡張できる。以下の議論においては は 行 列の行列であり、 は未定のままであると仮定する。 と が共に 行 列の行列である時の推定量は適切に識別されている(英語版)と言われる。
それぞれの内生的要素 と操作変数の間の関係が以下のように与えられると仮定する。
最も一般的な操作変数による特定化は以下の推定量を用いる。
この特定化は、真のモデルにおいて が満たされる限り、サンプルサイズが大きくなれば真のパラメータへと近づいていく。
データを生成する過程において が満たされる限り、操作変数推定量の適切な使用により、パラメータ が識別される。操作変数法は を満たす一意なパラメータについて解くので、これは機能し、そしてゆえにサンプルサイズが大きくなるにつれ真のパラメータに近づいていく。
今、拡張を行う。興味のある方程式における共変数の数より操作変数の数の方が大きいとする。つまり は 行 列行列で であるとする。これはしばしば過剰識別のケースと呼ばれる。この場合、一般化モーメント法(GMM)を用いることができる。GMM推定量は以下のようになる。
ここで は射影行列であり、 を満たす。
この表現は、操作変数の数と興味のある方程式における共変数の数が一致する時に、最初の表現にまとめることができる。過剰識別の操作変数法はそれゆえに、適切に識別された場合の操作変数法の一般化の一つである。
ここで、 の場合について同値な過小識別(英語版)推定量が存在する。パラメータは線形方程式のシステムの解であるので、方程式 を用いた過小識別モデルは一意解を持たない。
二段階最小二乗法としての解釈
操作変数法による推定量を計算するために使用できる計算方法の一つが二段階最小二乗法(英: two-stage least-squares, 2SLS, TSLS)である。第一段階において、興味のある方程式において内生性を持つすべての説明変数を、方程式における外生的な共変数と除外されている操作変数を含んだ全てのモデルにおける外生的な変数で回帰する。そしてこの回帰における予測値が得られる。
第一段階: のすべての列を で回帰する。()
そして予測値を保存する。
第二段階では、内生変数をすべて第一段階での予測値に置き換える以外は、興味のある回帰は通常通り推定される。
第二段階: を第一段階における予測値で回帰する。
ここから以下が得られる。
通常の最小二乗法推定量は である。 と置き換え、 は対称なべき等行列とする。つまり、 である。すると
となる。
の結果的な推定量は上で示した表現と数値的に一致する。 の共分散行列を正しく計算するためには、第二段階のモデルにおける残差二乗和について微修正が必要である。
ノンパラメトリック分析
構造方程式の形式が未知の時、操作変数 は以下の方程式を通して依然として定義可能である。
ここで と は2つの任意な関数で は からは独立である。線形モデルと異なり、 と の測定は の に対する平均因果効果(英: average causal effect, ACE)の識別を可能としない。
Balke and Pearl (1997) はACEの狭い境界を導出し、その境界はACEの符号と大きさについて価値ある情報を提供しうることを示した[13]。
線形分析では、 が の操作変数であるという仮定が正しいかどうか調べる検定はない。ただし が離散変数ならばそうではない。Pearl (2000) は全ての と について、 が上に上げた二つの方程式を満たすときはいつでも、以下の制約("操作不等式"、英: instrumental inequality)を満たさなくてはいけないことを示した[9]。
操作変数推定量の解釈において
上での例は興味のある因果効果は観測値の間で不変であることを仮定している、つまり、 が定数であるということを仮定している。一般的に、主体が異なれば、"処置" の変化に対する反応も異なる。この可能性を考慮に入れると、 の における変化の母集団における平均的な効果は与えられた部分母集団における平均的な効果とは異なるだろう。例えば、職業訓練プログラムの平均効果は、訓練を実際に受講した人々からなるグループと受講しなかった人々からなるグループとで実質的に異なるだろう。これらの理由により、操作変数法は、行動的な反応に対する暗黙的な仮定、もしくはより一般的に処置への反応と処置を受けるかどうかの傾向の間の相関についての仮定を課している[14]。
標準的な操作変数推定量は平均処置効果(英: average treatment effect, ATE)というよりは局所平均処置効果(英: local average treatment effect, LATE)を取り出すことができる。Imbens and Angrist (1994) は線形な操作変数推定量は弱い条件の下で局所平均処置効果の加重平均と見なせることを示した。ここでその加重は操作変数の変化に対する内生的な説明変数の弾力性に依存している。端的に言えば、観測された操作変数の変化に反応した部分母集団についてのみ変数の効果は表れ、操作変数の変化に最も反応した部分母集団が操作変数の大きさや程度に最も大きな影響を持つだろうということを意味している。
例えば、研究者がランドグラント大学の存在を所得の回帰における大学教育の操作変数として使う時、研究者は大学が存在していれば学位を取るが、存在していなければ学位を取らなかった部分母集団における大学の所得に対する影響を識別する。この実証研究では、追加的な仮定なしには、大学があろうとなかろうと学位を取る、もしくは取らない人々における大学の効果について研究者は何も言えない。
潜在的な問題
操作変数が興味のある方程式の誤差項と相関していると、操作変数推定量は一般的には一致推定量ではない。Bound, Jaeger, and Baker (1995) が記すように、"弱"操作変数の選択によりまた別の問題が起こる。弱操作変数とは、第一段階の方程式において内生的な説明変数の予測値としては不十分であるような操作変数のことである[15]。この場合、弱操作変数による内生変数の予測は不十分で、予測値はほとんど変動しない。結果として第二段階の方程式において内生変数を置き換えるために弱操作変数を使ったとき、最終的な値を予測することが難しくなる。
上で議論した喫煙と健康の例における文脈では、喫煙状態がタバコ税の変動にほとんど反応しないのであれば、タバコ税は喫煙についての弱操作変数となる。もし高い税率によって人々がタバコをやめる(もしくは喫煙を始めない)ことがないのであれば、タバコ税の変動は健康に対する喫煙の影響について何も情報を持たない。もしタバコ税が喫煙に与える影響というより他の経路を通して健康に影響を与えるのであれば、タバコ税は操作変数としては不適格であるし、操作変数法は間違った結果を生みかねない。例えば、相対的に健康志向な人々がいる時と場所においては、高い税率のタバコ税の実施と、たとえタバコ税が低率のままであったとしても健康であろうする行動の両方がなされるだろう。そして、仮にもし喫煙が健康に何の影響も与えないとしても、健康とタバコ税の間に相関が見られるだろう。この場合、タバコ税と健康の間に観測された相関から健康に対するタバコの因果効果を推測するのは過ちであろう。
標本性質と仮説検定
共変数が外生的である時、最小二乗推定量の小標本における性質は、 で条件づけた推定量のモーメントを計算するという標準的な方法で得ることができる。共変数のいくつかが内生的で操作変数法を用いている時、推定量のモーメントによる単純な表現は得られなくなる。一般的に操作変数推定量は漸近的に望ましい性質のみを持ち、有限標本における性質は明らかではなく、推量も推定量の標本分布に漸近的に近似することをベースにしている。操作変数が興味のある方程式の誤差項と無相関で、かつ弱操作変数でないとしても、操作変数推定量の有限標本における性質は大したものは得られない。例えば、適切に識別されたモデルからはモーメントを持たない有限標本推定量が得られ、ゆえにこの推定量のバイアスについて言えることは何もないし、検定統計量の名目値も実質的に歪み、推定量は一般的にパラメータの真の値から離れたものになる[16]。
操作変数の強さの検定と過剰識別制約
内生的な共変数と操作変数は両方とも観測可能なので、操作変数の強さは直接的に評価できる[17]。内生的な説明変数が一つの場合によく使われる経験的な方法の一つが以下のようなものである。第一段階の回帰において除外されている操作変数が無関係であるという帰無仮説の下でのF検定統計量が10以上かどうかで判別する。
操作変数が興味のある方程式の誤差項と相関していないという仮説は、適切に識別されたモデルでは検定不可能である。もしモデルが過剰識別ならば、この仮説を検定するために用いることのできる利用可能な情報がある。これらの過剰識別制約の最も一般的な検定で、サーガン-ハンセン検定(英語版)と呼ばれるものは、もし操作変数が本当に外生的ならば、回帰残差は外生変数とは無相関だろうという観察に基づいている[18]。サーガン-ハンセン検定統計量は回帰残差を外生的な変数に対し最小二乗法で回帰した際の (決定係数に観測値の数を掛けたもの)として計算できる。この検定統計量(の分布)は誤差項は操作変数と無相関であるという帰無仮説の下で自由度 のカイ二乗分布に漸近的に収束する。
脚注・参照文献
- ^ Imbens, G.; Angrist, J. (1994), “Identification and estimation of local average treatment effects”, Econometrica 62 (2): 467–476, JSTOR 2951620, https://jstor.org/stable/2951620
- ^ Bullock, J. G.; Green, D. P.; Ha, S. E. (2010). “Yes, But What’s the Mechanism? (Don’t Expect an Easy Answer)”. Journal of Personality and Social Psychology 98 (4): 550–558. doi:10.1037/a0018933.
- ^ https://www.stata.com/meeting/5nasug/wiv.pdf
- ^ The Fall of OLS in Structural Estimation, doi:10.2307/2663184 (inactive 23 March 2015), JSTOR 2663184。
- ^ Stock, James H.; Trebbi, Francesco (2003). "Retrospectives: Who Invented Instrumental Variable Regression?". Journal of Economic Perspectives. 17 (3): 177–194. doi:10.1257/089533003769204416。
- ^ Reiersøl, Olav (1945). Confluence Analysis by Means of Instrumental Sets of Variables. Arkiv for Mathematic, Astronomi, och Fysik. 32A. Uppsala: Almquist & Wiksells. OCLC 793451601
- ^ Bowden, R.J.; Turkington, D.A. (1984). Instrumental Variables. Cambridge, England: Cambridge University Press
- ^ 証明については [1]を参照。
- ^ a b c Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press. ISBN 0-521-89560-X
- ^ Leigh, J. P.; Schembri, M. (2004), “Instrumental Variables Technique: Cigarette Price Provided Better Estimate of Effects of Smoking on SF-12”, Journal of Clinical Epidemiology 57 (3): 284–293, doi:10.1016/j.jclinepi.2003.08.006
- ^ Angrist, J.; Krueger, A. (2001), “Instrumental Variables and the Search for Identification: From Supply and Demand to Natural Experiments”, Journal of Economic Perspectives 15 (4): 69–85, doi:10.1257/jep.15.4.69
- ^ Davidson, Russell; Mackinnon, James (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. ISBN 0-19-506011-3
- ^ Balke, A.; Pearl, J. (1997). “Bounds on treatment effects from studies with imperfect compliance”. Journal of the American Statistical Association 92 (439): 1172–1176. doi:10.1080/01621459.1997.10474074.
- ^ Heckman, J. (1997). “Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations”. Journal of Human Resources 32 (3): 441–462. JSTOR 146178.
- ^ Bound, J.; Jaeger, D. A.; Baker, R. M. (1995). “Problems with Instrumental Variables Estimation when the Correlation between the Instruments and the Endogenous Explanatory Variable is Weak”. Journal of the American Statistical Association 90 (430): 443. doi:10.1080/01621459.1995.10476536.
- ^ Nelson, C. R.; Startz, R. (1990). “Some Further Results on the Exact Small Sample Properties of the Instrumental Variable Estimator”. Econometrica 58 (4): 967–976. JSTOR 2938359.
- ^ Stock, J.; Wright, J.; Yogo, M. (2002). “A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments”. Journal of the American Statistical Association 20 (4): 518–529. doi:10.1198/073500102288618658.
- ^ Hayashi, Fumio (2000). “Testing Overidentifying Restrictions”. Econometrics. Princeton: Princeton University Press. pp. 217–221. ISBN 0-691-01018-8. https://books.google.com/books?id=QyIW8WUIyzcC&pg=PA217
発展的参考文献
- Greene, William H. (2008). Econometric Analysis (Sixth ed.). Upper Saddle River: Pearson Prentice-Hall. pp. 314–353. ISBN 978-0-13-600383-0
- Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 711–736. ISBN 978-0-07-337577-9
- Wooldridge, Jeffrey M. (2013). Introductory Econometrics: A Modern Approach (Fifth international ed.). Mason, OH: South-Western. pp. 490–528. ISBN 978-1-111-53439-4
関連項目
外部リンク
- [2] Layman による操作変数法の説明
- [3] ダニエル・マクファデンの教科書の第4章
- Econometrics lecture (topic: instrumental variable) - YouTube Mark Thoma による YouTube ビデオ
- Econmetrics lecture (topic: two-stages least square) - YouTube Mark Thoma による YouTube ビデオ
- ivpack: Instrumental Variable Estimation - CRAN











































































![{\displaystyle {\text{ACE}}=\Pr(y\mid {\text{do}}(x))=\operatorname {E} _{u}[f(x,u)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6ea36b8f79d0df3bb0e66e1b9273b9c9ae67edb)

![{\displaystyle \max _{x}\sum _{y}[\max _{z}\Pr(y,x\mid z)]\leq 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b089badc50cd6306cc6c673f45027813e1ebc23e)








