Gram–Schmidt-eljárás

A főként a lineáris algebrában és a numerikus analízisben használatos Gram–Schmidt-ortogonalizálás (avagy Gram–Schmidt-eljárás, esetleg Gram–Schmidt-féle ortogonalizálási eljárás) egy skalárszorzatos tér egy véges, lineárisan független {v_j} vektorrendszerét alakítja át egy olyan {u_j} vektorrendszerré, melynek elemei páronként merőlegesek egymásra (a skalárszorzatra vonatkozóan), más szóval ortogonálisak, és a két vektorrendszer ugyanazt az alteret feszíti ki az említett skalárszorzatos térben.^[1]

A módszert Jørgen Pedersen Gram és Erhard Schmidt után nevezték el, bár korábban Laplace-nál is szerepelt az eljárás.^[2] A Gram–Schmidt-ortogonalizálás egy általánosításának tekinthető a Lie-csoportok elméletében szereplő Iwasawa-dekompozíció.^[3]

Az eljárás alkalmazható például a reguláris mátrixok QR-felbontásánál.^[4]

A Gram–Schmidt-eljárás

Az egydimenziós altérre vetítés

Pre-Hilbert-térben (skalárszorzatos térben) az u nemnulla vektor alterébe merőlegesen vetít a

${\displaystyle \mathrm {proj} _{\mathbf {u} }\,\mathbf {x} =\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\mathbf {u} }{\|\mathbf {u} \|^{2}}}}$

leképezés, ahol <u, x> a két vektor skaláris szorzatát jelöli. A projekciótételből következik ugyanis, hogy pre-Hilbert-térben, ha létezik olyan y vektor az u kifeszítette altérben, hogy minden λ ∈ C(ill. R)-re

${\displaystyle \|\mathbf {x} -\mathbf {y} \|\leq \|\mathbf {x} -\lambda .\mathbf {u} \|\,}$

akkor az ilyen y-t egyértelműen jellemzi az, hogy minden λ ∈ C (illetve R)-re:

${\displaystyle \langle \mathbf {x} -\mathbf {y} ,\lambda .\mathbf {u} \rangle =0}$

És valóban létezik ilyen y éspedig pont a fenti projekció, ugyanis

${\displaystyle \left\langle \mathbf {x} -\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\mathbf {u} }{\|\mathbf {u} \|^{2}}},\lambda .\mathbf {u} \right\rangle =\langle \mathbf {x} ,\lambda .\mathbf {u} \rangle -\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\lambda .\mathbf {u} ^{2}}{\|\mathbf {u} \|^{2}}}=\langle \mathbf {x} ,\lambda .\mathbf {u} \rangle -\langle \lambda .\mathbf {u} ,\mathbf {x} \rangle \cdot 1=0}$

Az eljárás

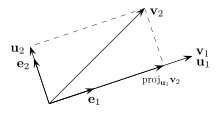
Legyen {v₁, ... , v_n } lineárisan független vektorrendszer. Azt az {u₁, ... , u_n } vektorrendszert, melynek elemei páronként merőlegesek és Span(v₁, ... , v_n) = Span(u₁, ... , u_n) (azaz ugyanazt az alteret feszítik ki, ugyanaz a generált Span(...) részalgebrájuk) a következőképpen kapjuk. Legyen u₁=v₁. Vetítsük v₂-t merőlegesen u₁-re, legyen ez w₂. Ekkor u₂ = v₂ – w₂. Tegyük ezt v₃-mal és u₁-vel illetve u₂-vel ... Ha ortonormált bázist akarunk, akkor osszuk le az u_k-kat a hosszukkal.

	${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1},}$		${\displaystyle \mathbf {e} _{1}={\mathbf {u} _{1} \over \|\mathbf {u} _{1}\|}}$
	${\displaystyle \mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{2},}$		${\displaystyle \mathbf {e} _{2}={\mathbf {u} _{2} \over \|\mathbf {u} _{2}\|}}$
	${\displaystyle \mathbf {u} _{3}=\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{2}}\,\mathbf {v} _{3},}$		${\displaystyle \mathbf {e} _{3}={\mathbf {u} _{3} \over \|\mathbf {u} _{3}\|}}$
	${\displaystyle \mathbf {u} _{4}=\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{2}}\,\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{3}}\,\mathbf {v} _{4},}$		${\displaystyle \mathbf {e} _{4}={\mathbf {u} _{4} \over \|\mathbf {u} _{4}\|}}$
	${\displaystyle \vdots }$		${\displaystyle \vdots }$
	${\displaystyle \mathbf {u} _{n}=\mathbf {v} _{n}-\sum _{k=1}^{n-1}\mathrm {proj} _{\mathbf {u} _{k}}\,\mathbf {v} _{n},}$		${\displaystyle \mathbf {e} _{n}={\mathbf {u} _{n} \over \|\mathbf {u} _{n}\|}}$

Helyesség

Annak az igazolása, hogy az eljárás valóban a kívánt eredményt adja a következő.^[5]

Először belátjuk, hogy az {u_k} vektorrendszer bázisa a {v_k} vektorrendszer által kifeszített L lineáris altérnek. Mivel L dimenziója a feltevés miatt éppen |{v_k}| = n, ezért elég belátni, hogy {u_k} generálja L-et. Tudjuk:

${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1}}$

${\displaystyle \mathbf {u} _{2}=\mathbf {v} _{2}-\lambda _{21}\mathbf {u} _{1}}$

${\displaystyle \mathbf {u} _{3}=\mathbf {v} _{3}-\lambda _{32}\mathbf {u} _{2}-\lambda _{31}\mathbf {u} _{1}}$

${\displaystyle \vdots }$

${\displaystyle \mathbf {u} _{n}=\mathbf {v} _{n}-\sum _{k=1}^{n-1}\lambda _{nk}{\mathbf {u} _{k}}}$

alkalmas λ_ij számokkal. Valójában tetszőleges λ_ij-kre generálja {u_k} az L-et, mert minden k-ra v_k előáll az u₁, ... , u_k-k lineáris kombinációjaként, azaz előállítják az összes bázisvektort, melyek viszont előállítják L összes elemét.

Másodszor belátjuk, hogy minden k = 1, ..., n-re az algoritmus által előállított {u₁,...,u_k} ortogonális, azaz

${\displaystyle \langle \mathbf {u} _{i},\mathbf {u} _{j}\rangle \left\{{\begin{matrix}\neq 0,&\mathrm {ha} &i=j\\=0,&\mathrm {ha} &i\neq j\end{matrix}}\right.}$

k=1 esetén az egyetlen nemnulla u teljesíti az ortogonalitási kritériumot. Ha 1, ..., k–1 már teljesíti a páronkénti ortogonalitást, akkor az u_k vektor mindegyik addigira merőleges, mert

${\displaystyle \langle \mathbf {u} _{i},\mathbf {u} _{k}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}-\sum _{j=1}^{k-1}\lambda _{kj}{\mathbf {u} _{j}}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -\sum _{j=1}^{k-1}\lambda _{kj}\langle \mathbf {u} _{i},\mathbf {u} _{j}\rangle =}$

${\displaystyle =\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -\lambda _{ki}\langle \mathbf {u} _{i},\mathbf {u} _{i}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -{\frac {\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle }{\|\mathbf {u} _{i}\|^{2}}}\langle \mathbf {u} _{i},\mathbf {u} _{i}\rangle =0}$,

hiszen az algoritmusból kiolvasva éppen

${\displaystyle \lambda _{ki}={\frac {\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle }{\|\mathbf {u} _{i}\|^{2}}}\,}$.

Megjegyzések

• Az eljárás általános k-adik lépésének formuláját így is írhatjuk:

${\displaystyle \mathbf {v} _{k}=\mathbf {u} _{k}+\sum _{i=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{i}}\,\mathbf {v} _{k}}$.

Eszerint ha már megvan az {u₁, ..., u_k–1} ortogonális rendszer, akkor a k-adik lépésben nem mást teszünk, mint vesszük a v_k vektor új, már meglévő báziselemekre eső merőleges vetületét és kiválasztjuk, hogy melyik u_k vektor az, amelyiket a vetületekhez adva v_k előáll. Míg a projekciótétel, lévén tiszta egzisztenciatétel, csak azt állítja, hogy létezik ilyen vektor, addig a Gram–Schmidt-eljárás konstruktívan adja meg a vetületet, éspedig:

${\displaystyle \mathbf {m} _{0}=\mathbf {v} _{k}-\mathbf {u} _{k}=\sum _{i=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{i}}\,\mathbf {v} _{k}}$.

A helyességi gondolatmenetben pont azt látjuk be, hogy a v_k – m₀ vektor merőleges a Span({u₁, ..., u_k–1}) altérre, hisz mindegyik bázisvektorára merőleges.

• Végtelen dimenziós altér esetén szintén alkalmazható az eljárás, azzal az eredménnyel, hogy az előállított (u₁, ..., u_k, ...) sorozatban bármely k-ig az u₁, ..., u_k vektorok páronként ortogonálisak.

• Nemfüggetlen vektorrendszerre alkalmazva az eljárást az eredményben előbb-utóbb előáll a 0 vektor. Ha ugyanis a k-adik vektor már az előzőek által kifeszített altérben van, akkor a vektorból az altérre eső vetületét kivonva a 0-t kapjuk. A nemfüggetlen vektorok által kifeszített alteret is lehet azonban ortogonális vektorokkal előállítani, éspedig úgy, hogy az algoritmusban minden új bázisvektor esetén megnézzük, hogy 0-t ad-e és ha igen, a régi vektort elvetjük és folytatjuk egy másik elem előállításával. Ekkor az algoritmus eredménye annyi vektor lesz, amennyi az eredeti vektorrendszer rangja volt.

Példa

Vegyük az

${\displaystyle A={\begin{bmatrix}1&2&1\end{bmatrix}}\,}$

mátrix magterét^[6] mint R³ alterét és adjunk meg benne egy ortogonális bázist!

A feladatot az

${\displaystyle \mathbf {a} \mathbf {b} =\sum \limits _{i=1}^{3}\mathbf {a} _{i}\mathbf {b} _{i}}$

sztenderd skalárszorzat szerint végezzük el!

Megoldás:

A dimenziótétel szerint a magtér kétdimenziós, ugyanis dim(R³) = dim Ker A + dim Im A, de A oszlopai skalárok, így dim Im A = 1. A kétdimenziós magtérnek kételemű a bázisa. A magtér egy alkalmas bázisa lehet az {v₁ = (2, -1, 0), v₂ = (1, 0, -1)}, mert a két vektor nyilvánvalóan lineárisan független, és mindkettő magtérbeli, mivel

${\displaystyle {\begin{bmatrix}1&2&1\end{bmatrix}}\cdot {\begin{bmatrix}2&1\\-1&0\\0&-1\end{bmatrix}}={\begin{bmatrix}0&0\end{bmatrix}}}$.

Feladatunk most már a bázisvektorok oszlopmátrixának ortogonalizálása. Alkalmazzuk az eljárást {v₁, v₂}-re!

${\displaystyle \mathbf {u} _{1}=\mathbf {v} _{1}={\begin{bmatrix}2\\-1\\0\end{bmatrix}}}$,

${\displaystyle \mathrm {proj} _{\mathbf {u} _{1}}\mathbf {v} _{2}=\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle {\frac {\mathbf {u} _{1}}{\|\mathbf {u} _{1}\|^{2}}}={\frac {2\cdot 1+(-1)\cdot 0+0\cdot (-1)}{2^{2}+(-1)^{2}+0^{2}}}{\begin{bmatrix}2\\-1\\0\end{bmatrix}}={\frac {2}{5}}\cdot {\begin{bmatrix}2\\-1\\0\end{bmatrix}}={\begin{bmatrix}{\frac {4}{5}}\\-{\frac {2}{5}}\\0\end{bmatrix}}}$,

${\displaystyle \mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\mathbf {v} _{2}={\begin{bmatrix}1\\0\\-1\end{bmatrix}}-{\begin{bmatrix}{\frac {4}{5}}\\-{\frac {2}{5}}\\0\end{bmatrix}}={\begin{bmatrix}{\frac {1}{5}}\\{\frac {2}{5}}\\-1\end{bmatrix}}}$.

Ellenőrizzük vektoriális szorzattal! Mivel

${\displaystyle \mathrm {Ker} \,A=\{(x,y,z)\in \mathbf {R} ^{3}\mid x+2y+z=0\}\,}$,

ezért nincs más feladatunk, mint a

${\displaystyle x+2y+z=0\,}$

síkban lévő két merőleges vektort mondanunk. Legyen ugyanaz az első:

${\displaystyle \mathbf {u} _{1}={\begin{bmatrix}2\\-1\\0\end{bmatrix}}}$,

ez valóban a síkban van. Most vegyük az (1, 2, 1) normálvektor^[7] és az előbbi vektoriális szorzatát:

${\displaystyle \mathbf {u} _{1}={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\1&2&1\\2&-1&0\end{vmatrix}}=1\mathbf {i} +2\mathbf {j} -5\mathbf {k} }$,

ami valóban párhuzamos a fent kapott vektorral, éspedig az 5-szöröse. Ebből is világosan látható, hogy az ortogonális vektorrendszer nem egyértélmű (még akkor sem, ha egységvektorokat választunk bázisnak).

Jegyzetek

Források

• Freud Róbert: Lineáris algebra (ELTE Eötvös Kiadó, 1998)
• Szörényi Miklós: Szemléletes lineáris algebra - összefoglaló I. informatikusoknak PDF (SZE MTK jegyzet, 2005)
• A kétdimenziós és háromdimenziós eset számítógépes animációval
• MIT Linear Algebra Lecture on Gram-Schmidt (angolul)