Sinus hyperbolique

Le sinus hyperbolique est, en mathématiques, une fonction hyperbolique.

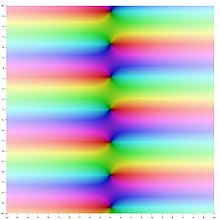
Définition

La fonction sinus hyperbolique, notée ${\displaystyle \sinh }$ (ou ${\displaystyle \operatorname {sh} }$)^[1] est la fonction complexe suivante :

${\displaystyle \sinh :z\mapsto {\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{2}}}$

où ${\displaystyle z\mapsto \mathrm {e} ^{z}}$ est l'exponentielle complexe.

La fonction sinus hyperbolique est la partie impaire de l'exponentielle complexe.

Dans la géométrie hyperbolique, la fonction sinus hyperbolique est un analogue de la fonction sinus de la géométrie euclidienne.

Propriétés

Propriétés générales

• ${\displaystyle \sinh }$ est continue et même holomorphe donc infiniment dérivable. Sa dérivée est la fonction cosinus hyperbolique notée ${\displaystyle \cosh }$.
• ${\displaystyle \sinh }$ est impaire.
• Les primitives de ${\displaystyle \sinh }$ sont ${\displaystyle \cosh +C}$, où ${\displaystyle C}$ est une constante d'intégration.
• La restriction de ${\displaystyle \sinh }$ à ℝ est strictement croissante, concave sur ${\displaystyle \left]-\infty ,0\right[}$ et convexe sur ${\displaystyle \left]0,+\infty \right[}$.

Propriétés trigonométriques

Des définitions des fonctions sinus et cosinus hyperbolique, on peut déduire les égalités suivantes :

${\displaystyle \mathrm {e} ^{z}=\cosh z+\sinh z}$

${\displaystyle \mathrm {e} ^{-z}=\cosh z-\sinh z}$

Ces égalités sont analogues aux formules d'Euler en trigonométrie classique.

De même que les coordonnées ${\displaystyle (\cos t,\sin t)}$ définissent un cercle, ${\displaystyle (\cosh t,\sinh t)}$ définissent la branche positive d'une hyperbole équilatère. On a en effet pour tout ${\displaystyle t}$ :

${\displaystyle \cosh ^{2}t-\sinh ^{2}t=1}$.

D'autre part, pour ${\displaystyle x\in \mathbb {R} }$ :

${\displaystyle \sinh(\mathrm {i} x)={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2}}=\mathrm {i} \sin(x)}$ , d'où ${\displaystyle \sinh(x)=-\mathrm {i} \sin(\mathrm {i} x)}$;

${\displaystyle \sinh(x+y)=\sinh(x)\cosh(y)+\cosh(x)\sinh(y)}$ , d'où ${\displaystyle \sinh x=2\sinh \left({\frac {x}{2}}\right)\cosh \left({\frac {x}{2}}\right)}$;

${\displaystyle \sinh x=x\prod _{n=1}^{\infty }{\cosh \left(x/2^{n}\right)}}$ (obtenu en itérant la formule précédente) ;

${\displaystyle \sinh ^{2}\left({\frac {x}{2}}\right)={\frac {\cosh(x)-1}{2}}}$.

L'utilisation de formules trigonométriques telles que ${\displaystyle \tan(2t)={\frac {2\tan t}{1-\tan ^{2}t}}}$ permet aussi d'obtenir des relations plus anecdotiques, telle que (pour tout réel ${\displaystyle x}$ non nul) :

${\displaystyle \sinh(x)={\frac {-1}{\tan \left(2\arctan \left(\mathrm {e} ^{x}\right)\right)}}}$ ;

voir également l'article Gudermannien.

Développement en série de Taylor

La série de Taylor en 0 de la fonction ${\displaystyle \sinh }$ converge sur ℂ tout entier et est donnée par :

${\displaystyle \sinh z=z+{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}+\dots =\sum _{n=0}^{+\infty }{\frac {z^{2n+1}}{(2n+1)!}}}$.

Valeurs

Quelques valeurs de ${\displaystyle \sinh }$ :

• ${\displaystyle \sinh(0)=0}$ ;
• ${\displaystyle \sinh(1)={\frac {\mathrm {e} ^{2}-1}{2\mathrm {e} }}}$ ;
• ${\displaystyle \sinh(\mathrm {i} )=\mathrm {i} \sin(1)}$.

Zéros

Tous les zéros de ${\displaystyle \sinh }$ sont des imaginaires purs : ${\displaystyle \forall z\in \mathbb {C} \quad \sinh(z)=0\Leftrightarrow z\in \mathrm {i} \pi \mathbb {Z} }$.

Fonction réciproque

${\displaystyle \sinh }$ admet une fonction réciproque, notée ${\displaystyle \operatorname {arsinh} }$ (ou ${\displaystyle \operatorname {argsinh} }$ ou ${\displaystyle \operatorname {argsh} }$ ou parfois ${\displaystyle \operatorname {sinh^{-1}} }$)^[2], et nommée argument sinus hyperbolique. Il s'agit d'une fonction multiforme complexe. Sa branche principale est généralement^[3] choisie en posant comme coupure les demi-droites ${\displaystyle \left]-\infty \mathrm {i} ,-\mathrm {i} \right]}$ et ${\displaystyle \left[\mathrm {i} ,+\infty \mathrm {i} \right[}$ :

${\displaystyle \operatorname {arsinh} (z)=\log \left(z+{\sqrt {1+z^{2}}}\right)}$,

où ${\displaystyle \log }$ et ${\displaystyle {\sqrt {~}}}$ sont les déterminations principales du logarithme complexe de la racine carrée complexe. En effet, si ${\displaystyle \sinh Z=z}$ alors ${\displaystyle \cosh ^{2}Z=1+z^{2}}$, or ${\displaystyle \mathrm {e} ^{Z}=\sinh Z+\cosh Z}$.

La restriction-corestriction de sinh de ℝ dans ℝ admet donc pour réciproque : ${\displaystyle \operatorname {arsinh} (x)=\ln \left(x+{\sqrt {1+x^{2}}}\right)}$.

Cette branche principale est holomorphe sur le disque unité ${\displaystyle |z|<1}$ et y admet le développement en série entière :

${\displaystyle {\rm {arsinh}}(z)=z+\sum _{n=1}^{+\infty }(-1)^{n}{\frac {1.3.5\dots (2n-1)}{2.4.6\dots (2n).(2n+1)}}z^{2n+1}}$.

Voir aussi

• Cosinus hyperbolique
• Tangente hyperbolique
• Produit infini

Références

• Portail de l'analyse