Beta-jakauma Tiheysfunktio Kertymäfunktio Merkintä B e t a ( α , β ) {\displaystyle Beta(\alpha ,\beta )} Parametrit α , β ∈ [ 0 , ∞ ) {\displaystyle \alpha ,\beta \in [0,\infty )} Määrittelyjoukko x ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]} Tiheysfunktio 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 {\displaystyle {\frac {1}{B(\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1}} Kertymäfunktio I x ( α , β ) ) {\displaystyle I_{x}(\alpha ,\beta ))} Odotusarvo α α + β {\displaystyle {\frac {\alpha }{\alpha +\beta }}} Moodi α − 1 α + β − 2 {\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}} Varianssi α β ( α + β ) 2 ( α + β + 1 ) {\displaystyle {\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}} Vinous 2 ( β − α ) α + β + 1 ( α + β + 2 ) α β {\displaystyle {\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}} Huipukkuus 6 [ α 3 + α 2 ( 1 − 2 β ) + β 2 ( β + 1 ) − 2 α β ( β + 2 ) ] α β ( α + β + 2 ) ( α + β + 3 ) {\displaystyle {\frac {6[\alpha ^{3}+\alpha ^{2}(1-2\beta )+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}} Entropia ln B ( α , β ) − ( α − 1 ) ψ ( α ) − ( β − 1 ) ψ ( β ) + ( α + β − 2 ) ψ ( α + β ) {\displaystyle {\begin{matrix}\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )\\[0.5em]+(\alpha +\beta -2)\psi (\alpha +\beta )\end{matrix}}} Momentit generoiva funktio 1 + ∑ k = 1 ∞ ( ∏ r = 0 k − 1 α + r α + β + r ) t k k ! {\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}} Karakteristinen funktio 1 F 1 ( α ; α + β ; i t ) {\displaystyle {}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!} Fisherin informaatiomatriisi var [ ln X ] cov [ ln X , ln ( 1 − X ) ] cov [ ln X , ln ( 1 − X ) ] var [ ln ( 1 − X ) ] {\displaystyle {\begin{matrix}\\\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X,\ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{matrix}}}
Beta-jakauma [1] β − {\displaystyle \beta -} [2] todennäköisyyslaskennassa ja tilastotieteessä jatkuvan satunnaismuuttujan todennäköisyysjakauma , jota käytetään bayesilaisessa todennäköisyyslaskennassa. Koska Beta-jakaumaa voi parametrisoida monella eri tavalla, sitä voidaan kutsua jakaumaperheeksi. Sen avulla voidaan esittää lähes kaikki äärelliselle välille konsentroituneet jakaumat.[1] [2]
Jos satunnaismuuttuja X {\displaystyle X} α {\displaystyle \alpha } β {\displaystyle \beta }
X ∼ B e t a ( α , β ) {\displaystyle X\sim Beta(\alpha ,\beta )} [1] ∼ B e ( α , β ) {\displaystyle \sim Be(\alpha ,\beta )} ∼ β α , β . {\displaystyle \sim \beta _{\alpha ,\beta }.} Todennäköisyysjakauma Satunnaismuuttujalla X {\displaystyle X} Ω = {\displaystyle \Omega =} α {\displaystyle \alpha } β {\displaystyle \beta }
f X ( x ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 , {\displaystyle f_{X}(x)={\frac {1}{B(\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1},} [1] missä niin sanottu beta-funktio on
B ( α , β ) = ∫ 0 1 t α − 1 ( 1 − t ) β − 1 d t = Γ ( α ) Γ ( β ) Γ ( α + β ) , {\displaystyle B(\alpha ,\beta )=\int _{0}^{1}t^{\alpha -1}(1-t)^{\beta -1}dt={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}},} [1] jossa Γ ( t ) {\displaystyle \Gamma (t)} gammafunktio . Beta-funktion tarkoituksena on "normalisoida" beta-jakauma niin, että sen tiheysfunktion määrätty integraali koko reaalialueen yli on tasan yksi.[3]
Toisinaan joskus parametrien arvoista vähennetään yksi ( α ′ = α − 1 {\displaystyle \scriptstyle \alpha '=\alpha -1} β ′ = β − 1 {\displaystyle \scriptstyle \beta '=\beta -1} momenttifunktion kaavat yksinkertaistuisivat hieman.[4]
Beta-jakauman tiheysfunktiolla on seuraavanlaisia ominaisuuksia:[1]
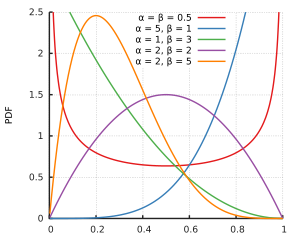
f X ( x ) > 0 {\displaystyle f_{X}(x)>0} x ∈ [ 0 , 1 ] {\displaystyle x\in [0,1]} Jos α > 1 {\displaystyle \alpha >1} β = 1 {\displaystyle \beta =1} f X ( x ) {\displaystyle f_{X}(x)} aidosti kasvava ja sen maksimikohta on välin päätepisteessä x = 1. {\displaystyle x=1.} Jos α = 1 {\displaystyle \alpha =1} β > 1 {\displaystyle \beta >1} f X ( x ) {\displaystyle f_{X}(x)} aidosti vähenevä ja sen maksimikohta on välin päätepisteessä x = 0. {\displaystyle x=0.} Jos α > 1 {\displaystyle \alpha >1} β > 1 {\displaystyle \beta >1} f X ( x ) {\displaystyle f_{X}(x)} x = α − 1 α + β − 2 . {\displaystyle x={\frac {\alpha -1}{\alpha +\beta -2}}.} Jos α < 1 {\displaystyle \alpha <1} β < 1 {\displaystyle \beta <1} f X ( x ) {\displaystyle f_{X}(x)} x = 0 {\displaystyle x=0} x = 1. {\displaystyle x=1.} f X ( x ) {\displaystyle f_{X}(x)} α = β . {\displaystyle \alpha =\beta .} Beta-jakauman kertymäfunktion lauseketta ei ole mahdollista kirjoittaa eksplisiittiseen muotoon , koska sen tiheysfunktion integraalifunktiota ei voi kirjoittaa lausekkeeksi alkeisfunktioiden avulla. Ne onkin tapana esittää vain numeerisessa muodossa aivan kuten toimitaan normaalijakaumassakin .[1]
Tunnusluvut ja momentit Momenttifunktio Momenttifunktio eli momentit generoiva funktio saadaan määritelmästä
M ( t ) = E ( e t X ) = 1 B ( α , β ) ∫ 0 1 e t x x α − 1 ( 1 − x ) β − 1 d x . {\displaystyle M(t)=E(e^{tX})={\frac {1}{B(\alpha ,\beta )}}\int _{0}^{1}e^{tx}x^{\alpha -1}(1-x)^{\beta -1}\,dx.} Sen avulla voidaan määritellä origomomentit ja keskusmomentit . Origomomenttien yleinen muoto on
μ n = E ( X n ) = Γ ( α + β ) Γ ( α + n ) Γ ( α + β + n ) Γ ( α ) , {\displaystyle \mu _{n}=E(X^{n})={\frac {\Gamma (\alpha +\beta )\Gamma (\alpha +n)}{\Gamma (\alpha +\beta +n)\Gamma (\alpha )}},} [4] ja koska gammafunktiolla on Γ ( α + 1 ) = α Γ ( α ) {\displaystyle \Gamma (\alpha +1)=\alpha \Gamma (\alpha )}
E ( X ) = E ( X 1 ) = Γ ( α + β ) Γ ( α + 1 ) Γ ( α + β + 1 ) Γ ( α ) = Γ ( α + β ) α Γ ( α ) ( α + β ) Γ ( α + β ) Γ ( α ) = α α + β {\displaystyle E(X)=E(X^{1})={\frac {\Gamma (\alpha +\beta )\Gamma (\alpha +1)}{\Gamma (\alpha +\beta +1)\Gamma (\alpha )}}={\frac {\Gamma (\alpha +\beta )\alpha \Gamma (\alpha )}{(\alpha +\beta )\Gamma (\alpha +\beta )\Gamma (\alpha )}}={\frac {\alpha }{\alpha +\beta }}} ja
E ( X 2 ) = Γ ( α + β ) Γ ( α + 2 ) Γ ( α + β + 2 ) Γ ( α ) = Γ ( α + β ) ( α + 1 ) α Γ ( α ) ( α + β + 1 ) ( α + β ) Γ ( α + β ) Γ ( α ) = α ( α + 1 ) ( α + β ) ( α + β + 1 ) . {\displaystyle E(X^{2})={\frac {\Gamma (\alpha +\beta )\Gamma (\alpha +2)}{\Gamma (\alpha +\beta +2)\Gamma (\alpha )}}={\frac {\Gamma (\alpha +\beta )(\alpha +1)\alpha \Gamma (\alpha )}{(\alpha +\beta +1)(\alpha +\beta )\Gamma (\alpha +\beta )\Gamma (\alpha )}}={\frac {\alpha (\alpha +1)}{(\alpha +\beta )(\alpha +\beta +1)}}.} Keskusmomenttien yleinen muoto on
μ n ′ = E ( ( X − μ ) n ) = ( − α α + β ) n ⋅ 2 F 1 ( α , − n ; α + β ; α + β α ) , {\displaystyle \mu '_{n}=E((X-\mu )^{n})=\left(-{\frac {\alpha }{\alpha +\beta }}\right)^{n}\cdot {}_{2}F_{1}\left(\alpha ,-n;\alpha +\beta ;{\frac {\alpha +\beta }{\alpha }}\right),} missä 2 F 1 {\displaystyle {}_{2}\!F_{1}} hypergeometrinen funktio .[4]
Ensimmäinen origomomentti voidaan laskea myös suoraan
μ = E ( X ) = ∫ 0 1 x f X ( x ) d x = ∫ 0 1 x 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 d x {\displaystyle \mu =E(X)=\int _{0}^{1}xf_{X}(x)\,dx=\int _{0}^{1}x{\frac {1}{B(\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1}\,dx} = 1 B ( α , β ) ∫ 0 1 x α ( 1 − x ) β − 1 d x = 1 B ( α , β ) B ( α + 1 , β ) {\displaystyle ={\frac {1}{B(\alpha ,\beta )}}\int _{0}^{1}x^{\alpha }(1-x)^{\beta -1}\,dx={\frac {1}{B(\alpha ,\beta )}}B(\alpha +1,\beta )} = Γ ( α + 1 ) Γ ( β ) Γ ( α + β + 1 ) ⋅ Γ ( α + β ) Γ ( α ) Γ ( β ) = α Γ ( α ) Γ ( β ) ( α + β ) Γ ( α + β ) ⋅ Γ ( α + β ) Γ ( α ) Γ ( β ) = α α + β . {\displaystyle ={\frac {\Gamma (\alpha +1)\Gamma (\beta )}{\Gamma (\alpha +\beta +1)}}\cdot {\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}={\frac {\alpha \Gamma (\alpha )\Gamma (\beta )}{(\alpha +\beta )\Gamma (\alpha +\beta )}}\cdot {\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}={\frac {\alpha }{\alpha +\beta }}.} [1] Tunnuslukuja Jakauman odotusarvo saadaan ensimmäisestä origomomentista
μ = E ( X ) = α α + β . {\displaystyle \mu =\operatorname {E} (X)={\frac {\alpha }{\alpha +\beta }}.} [4] Sen varianssi on taas suoraan toinen keskusmomentti
μ 2 ′ = Var ( X ) = σ 2 = α β ( α + β ) 2 ( α + β + 1 ) . {\displaystyle \mu '_{2}=\operatorname {Var} (X)=\sigma ^{2}={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}.} [3] [4] Jakauman tiheysfunktion vinous määritetään kahden keskumomentin avulla
g 1 = μ 3 ′ μ ′ 2 3 / 2 = 2 ( β − α ) α + β + 1 ( α + β + 2 ) α β . {\displaystyle g_{1}={\frac {\mu '_{3}}{{\mu '}_{2}^{3/2}}}={\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}.} [3] [5] [4] Vinous on nolla, mikä näkyy tasajakauman tiheysfunktion kuvaajasta, joka on täysin symmetrinen.
Jakauman huipukkuus määritetään kahden keskusmomentin avulla
γ 2 = μ ′ 4 μ ′ 2 2 − 3 = 6 [ α 3 + α 2 ( 1 − 2 β ) + β 2 ( β + 1 ) − 2 α β ( β + 2 ) ] α β ( α + β + 2 ) ( α + β + 3 ) . {\displaystyle \gamma _{2}={\frac {{\mu '}_{4}}{{\mu '}_{2}^{2}}}-3={\frac {6[\alpha ^{3}+\alpha ^{2}(1-2\beta )+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}.} [3] [6] [4] Negativinen huipukkuus näkyy tiheysfunktion kuvaajassa siten, että kuvaaja on "tasa- ja litteäpäinen" eikä terävää kärkeä esiinny ollenkaan.
Jakauman moodi sijaitsee välin [0,1] sisäpisteessä, kun α > 1 {\displaystyle \alpha >1} β > 1 {\displaystyle \beta >1}
M o = α − 1 α + β − 2 . {\displaystyle Mo={\frac {\alpha -1}{\alpha +\beta -2}}.} Jos α < 1 {\displaystyle \alpha <1} β < 1 {\displaystyle \beta <1} α = β = 1 {\displaystyle \alpha =\beta =1} tasajakauma ja kaikki pisteet ovat moodi.[3]
Esimerkkejä Tarkastellaan toistokoetta , jonka yksittäisen kolikonheiton arvoksi voi tulla vain "kruuna" tai "klaava" todennäköisyyksillä p {\displaystyle p} 1 − p {\displaystyle 1-p} n = 100 {\displaystyle n=100} X {\displaystyle X} binomijakaumaa X ∼ B i n ( 100 , p ) {\displaystyle X\sim Bin(100,p)} p {\displaystyle p} k = 60 {\displaystyle k=60} p ∼ B e t a ( 61 , 41 ) {\displaystyle p\sim Beta(61,41)} [7]
Edellinen ongelma on perinteisesti ratkaistu käyttäen normaalijakaumaa , mutta Beta-jakauma antaa silloin oikean tuloksen, kun se määritellään
p ∼ B e t a ( k + 1 , n − k + 1 ) . {\displaystyle p\sim Beta(k+1,n-k+1).} Normaalijakauma antaa harhaisen tuloksen, mikäli toistojen lukumäärä n {\displaystyle n} k / n {\displaystyle k/n} [7]
Beta-jakaumaa tulisi käyttää normaalijakauman sijasta approksimoitaessa binomijakaumaa epäsymmetrisissä tiheysjakauman tilanteissa. Esimerkiksi epäsymmetrisessä ja kahta arvoa antavassa satunnaistapauhtumassa kannattaa käyttää diskreetin binomijakauman approksimoimiseksi jatkuvaa Beetta-jakaumaa. Yleensä binomijakaumaa approksimoidaan normaalijakaumalla, mutta se ei toimi kunnolla, kun toista arvoa esiintyy tuntuvasti enemmän kuin toista.[7]
Beta-jakaumaa voidaan käyttää arvioitaessa tasajakaumien U i ∼ U ( 0 , 1 ) {\displaystyle U_{i}\sim U(0,1)} n satunnaismuuttujalle U i {\displaystyle U_{i}} U 1 , {\displaystyle U_{1},} U 2 {\displaystyle U_{2}} , . . . , {\displaystyle ,...,} U n {\displaystyle U_{n}} U ( i ) , {\displaystyle U_{(i)},} i :nnes. (eli U ( 1 ) {\displaystyle U_{(1)}} U ( 2 ) {\displaystyle U_{(2)}} U ( n ) {\displaystyle U_{(n)}} U ( k ) ∼ B e t a ( k , n + 1 − k ) {\displaystyle U_{(k)}\sim Beta(k,n+1-k)} k = 1 , 2 , . . . , n {\displaystyle k=1,2,...,n} [8]
Muut jakaumat Beta-jakaumasta saadaan tasajakauma , mikäli parametrit ovat molemmat yksi
X ∼ B e t a ( 1 , 1 ) ∼ U ( 0 , 1 ) . {\displaystyle X\sim Beta(1,1)\sim U(0,1).} [2] Lähteet ↑ a b c d e f g h Mellin, Ilkka: Todennäköisyysjakaumat, s. 407−410, luentomonisteesta Todennäköisyyslaskenta, Aalto-yliopisto, 2006 ↑ a b c Rahiala, Markku : Satunnaismallien teoria (Arkistoitu – Internet Archive), s. 21−22, Oulun yliopisto, 2002↑ a b c d e Johnson, Paul & Beverlin, Matt: Beta Distribution, 2013 ↑ a b c d e f g Weisstein, Eric W.: Beta Distribution (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi) ↑ Weisstein, Eric W.: Skewness (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi) ↑ Weisstein, Eric W.: Kurtosis (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi) ↑ a b c Stich, Slater: Use the Beta Distribution ↑ Laurent, Stéphane: The Beta distribution also appears as an order statistic... Aiheesta muualla Commons https://noppa.aalto.fi/noppa/kurssi/mat-1.3621/luennot/Mat-1_3621_todennakoisyyslaskennan_kertausta_.pdf[vanhentunut linkki] http://doingbayesiandataanalysis.blogspot.fi/2012/06/beta-distribution-parameterized-by-mode.html http://users.iems.northwestern.edu/~ajit/beta.pdf http://www.epixanalytics.com/modelassist/CrystalBall/Model_Assist.htm#Distributions/Continuous_distributions/Beta.htm (Arkistoitu – Internet Archive)
Diskreettejä jakaumia Jatkuvia jakaumia Moniulotteisia jakaumia Dirichlet-jakauma Moniulotteinen Studentin t-jakauma Multinomijakauma Multinormaalijakauma




![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)






![{\displaystyle {\frac {6[\alpha ^{3}+\alpha ^{2}(1-2\beta )+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/626a31af2c341c68203ff1c65a6c43548ba570fc)
![{\displaystyle {\begin{matrix}\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )\\[0.5em]+(\alpha +\beta -2)\psi (\alpha +\beta )\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c89e36ccbf7522eba17d6e5ddb267e7cef46b8e)


![{\displaystyle {\begin{matrix}\\\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X,\ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1acc13ea0028ec81e619308a5f163484b225412)







































![{\displaystyle \gamma _{2}={\frac {{\mu '}_{4}}{{\mu '}_{2}^{2}}}-3={\frac {6[\alpha ^{3}+\alpha ^{2}(1-2\beta )+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4a1ddb02731da3c45ef3a7e6fb1d8785de755b)

































