Steiner conic

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.

The usual definition of a conic uses a quadratic form (see Quadric (projective geometry)). Another alternative definition of a conic uses a hyperbolic polarity. It is due to K. G. C. von Staudt and sometimes called a von Staudt conic. The disadvantage of von Staudt's definition is that it only works when the underlying field has odd characteristic (i.e., ${\displaystyle Char\neq 2}$).

Definition of a Steiner conic

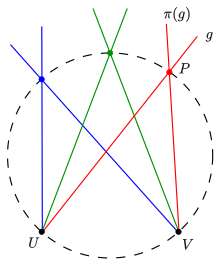
• Given two pencils ${\displaystyle B(U),B(V)}$ of lines at two points ${\displaystyle U,V}$ (all lines containing ${\displaystyle U}$ and ${\displaystyle V}$ resp.) and a projective but not perspective mapping ${\displaystyle \pi }$ of ${\displaystyle B(U)}$ onto ${\displaystyle B(V)}$. Then the intersection points of corresponding lines form a non-degenerate projective conic section^[1][2][3][4] (figure 1)

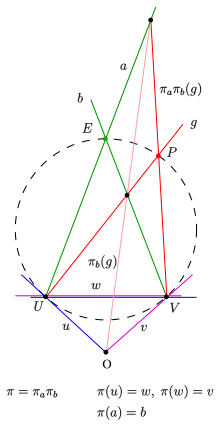
A perspective mapping ${\displaystyle \pi }$ of a pencil ${\displaystyle B(U)}$ onto a pencil ${\displaystyle B(V)}$ is a bijection (1-1 correspondence) such that corresponding lines intersect on a fixed line ${\displaystyle a}$, which is called the axis of the perspectivity ${\displaystyle \pi }$ (figure 2).

A projective mapping is a finite product of perspective mappings.

Simple example: If one shifts in the first diagram point ${\displaystyle U}$ and its pencil of lines onto ${\displaystyle V}$ and rotates the shifted pencil around ${\displaystyle V}$ by a fixed angle ${\displaystyle \varphi }$ then the shift (translation) and the rotation generate a projective mapping ${\displaystyle \pi }$ of the pencil at point ${\displaystyle U}$ onto the pencil at ${\displaystyle V}$. From the inscribed angle theorem one gets: The intersection points of corresponding lines form a circle.

Examples of commonly used fields are the real numbers ${\displaystyle \mathbb {R} }$, the rational numbers ${\displaystyle \mathbb {Q} }$ or the complex numbers ${\displaystyle \mathbb {C} }$. The construction also works over finite fields, providing examples in finite projective planes.

Remark: The fundamental theorem for projective planes states,^[5] that a projective mapping in a projective plane over a field (pappian plane) is uniquely determined by prescribing the images of three lines. That means that, for the Steiner generation of a conic section, besides two points ${\displaystyle U,V}$ only the images of 3 lines have to be given. These 5 items (2 points, 3 lines) uniquely determine the conic section.

Remark: The notation "perspective" is due to the dual statement: The projection of the points on a line ${\displaystyle a}$ from a center ${\displaystyle Z}$ onto a line ${\displaystyle b}$ is called a perspectivity (see below).^[5]

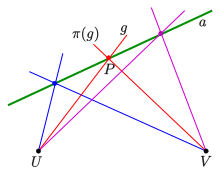
Example

For the following example the images of the lines ${\displaystyle a,u,w}$ (see picture) are given: ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$. The projective mapping ${\displaystyle \pi }$ is the product of the following perspective mappings ${\displaystyle \pi _{b},\pi _{a}}$: 1) ${\displaystyle \pi _{b}}$ is the perspective mapping of the pencil at point ${\displaystyle U}$ onto the pencil at point ${\displaystyle O}$ with axis ${\displaystyle b}$. 2) ${\displaystyle \pi _{a}}$ is the perspective mapping of the pencil at point ${\displaystyle O}$ onto the pencil at point ${\displaystyle V}$ with axis ${\displaystyle a}$. First one should check that ${\displaystyle \pi =\pi _{a}\pi _{b}}$ has the properties: ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$. Hence for any line ${\displaystyle g}$ the image ${\displaystyle \pi (g)=\pi _{a}\pi _{b}(g)}$ can be constructed and therefore the images of an arbitrary set of points. The lines ${\displaystyle u}$ and ${\displaystyle v}$ contain only the conic points ${\displaystyle U}$ and ${\displaystyle V}$ resp.. Hence ${\displaystyle u}$ and ${\displaystyle v}$ are tangent lines of the generated conic section.

A proof that this method generates a conic section follows from switching to the affine restriction with line ${\displaystyle w}$ as the line at infinity, point ${\displaystyle O}$ as the origin of a coordinate system with points ${\displaystyle U,V}$ as points at infinity of the x- and y-axis resp. and point ${\displaystyle E=(1,1)}$. The affine part of the generated curve appears to be the hyperbola ${\displaystyle y=1/x}$.^[2]

Remark:

1. The Steiner generation of a conic section provides simple methods for the construction of ellipses, parabolas and hyperbolas which are commonly called the parallelogram methods.
2. The figure that appears while constructing a point (figure 3) is the 4-point-degeneration of Pascal's theorem.^[6]

Steiner generation of a dual conic

Definitions and the dual generation

Dualizing (see duality (projective geometry)) a projective plane means exchanging the points with the lines and the operations intersection and connecting. The dual structure of a projective plane is also a projective plane. The dual plane of a pappian plane is pappian and can also be coordinatized by homogeneous coordinates. A nondegenerate dual conic section is analogously defined by a quadratic form.

A dual conic can be generated by Steiner's dual method:

• Given the point sets of two lines ${\displaystyle u,v}$ and a projective but not perspective mapping ${\displaystyle \pi }$ of ${\displaystyle u}$ onto ${\displaystyle v}$. Then the lines connecting corresponding points form a dual non-degenerate projective conic section.

A perspective mapping ${\displaystyle \pi }$ of the point set of a line ${\displaystyle u}$ onto the point set of a line ${\displaystyle v}$ is a bijection (1-1 correspondence) such that the connecting lines of corresponding points intersect at a fixed point ${\displaystyle Z}$, which is called the centre of the perspectivity ${\displaystyle \pi }$ (see figure).

A projective mapping is a finite sequence of perspective mappings.

It is usual, when dealing with dual and common conic sections, to call the common conic section a point conic and the dual conic a line conic.

In the case that the underlying field has ${\displaystyle \operatorname {Char} =2}$ all the tangents of a point conic intersect in a point, called the knot (or nucleus) of the conic. Thus, the dual of a non-degenerate point conic is a subset of points of a dual line and not an oval curve (in the dual plane). So, only in the case that ${\displaystyle \operatorname {Char} \neq 2}$ is the dual of a non-degenerate point conic a non-degenerate line conic.

Examples

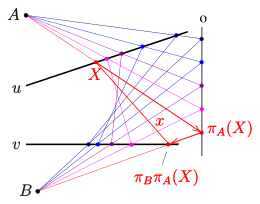
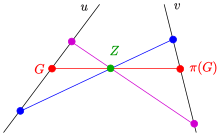
(1) Projectivity given by two perspectivities:
Two lines ${\displaystyle u,v}$ with intersection point ${\displaystyle W}$ are given and a projectivity ${\displaystyle \pi }$ from ${\displaystyle u}$ onto ${\displaystyle v}$ by two perspectivities ${\displaystyle \pi _{A},\pi _{B}}$ with centers ${\displaystyle A,B}$. ${\displaystyle \pi _{A}}$ maps line ${\displaystyle u}$ onto a third line ${\displaystyle o}$, ${\displaystyle \pi _{B}}$ maps line ${\displaystyle o}$ onto line ${\displaystyle v}$ (see diagram). Point ${\displaystyle W}$ must not lie on the lines ${\displaystyle {\overline {AB}},o}$. Projectivity ${\displaystyle \pi }$ is the composition of the two perspectivities: ${\displaystyle \ \pi =\pi _{B}\pi _{A}}$. Hence a point ${\displaystyle X}$ is mapped onto ${\displaystyle \pi (X)=\pi _{B}\pi _{A}(X)}$ and the line ${\displaystyle x={\overline {X\pi (X)}}}$ is an element of the dual conic defined by ${\displaystyle \pi }$.
(If ${\displaystyle W}$ would be a fixpoint, ${\displaystyle \pi }$ would be perspective.^[7])

(2) Three points and their images are given:
The following example is the dual one given above for a Steiner conic.
The images of the points ${\displaystyle A,U,W}$ are given: ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$. The projective mapping ${\displaystyle \pi }$ can be represented by the product of the following perspectivities ${\displaystyle \pi _{B},\pi _{A}}$:

1. ${\displaystyle \pi _{B}}$ is the perspectivity of the point set of line ${\displaystyle u}$ onto the point set of line ${\displaystyle o}$ with centre ${\displaystyle B}$.
2. ${\displaystyle \pi _{A}}$ is the perspectivity of the point set of line ${\displaystyle o}$ onto the point set of line ${\displaystyle v}$ with centre ${\displaystyle A}$.

One easily checks that the projective mapping ${\displaystyle \pi =\pi _{A}\pi _{B}}$ fulfills ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$. Hence for any arbitrary point ${\displaystyle G}$ the image ${\displaystyle \pi (G)=\pi _{A}\pi _{B}(G)}$ can be constructed and line ${\displaystyle {\overline {G\pi (G)}}}$ is an element of a non degenerate dual conic section. Because the points ${\displaystyle U}$ and ${\displaystyle V}$ are contained in the lines ${\displaystyle u}$, ${\displaystyle v}$ resp.,the points ${\displaystyle U}$ and ${\displaystyle V}$ are points of the conic and the lines ${\displaystyle u,v}$ are tangents at ${\displaystyle U,V}$.

Intrinsic conics in a linear incidence geometry

The Steiner construction defines the conics in a planar linear incidence geometry (two points determine at most one line and two lines intersect in at most one point) intrinsically, that is, using only the collineation group. Specifically, ${\displaystyle E(T,P)}$ is the conic at point ${\displaystyle P}$ afforded by the collineation ${\displaystyle T}$, consisting of the intersections of ${\displaystyle L}$ and ${\displaystyle T(L)}$ for all lines ${\displaystyle L}$ through ${\displaystyle P}$. If ${\displaystyle T(P)=P}$ or ${\displaystyle T(L)=L}$ for some ${\displaystyle L}$ then the conic is degenerate. For example, in the real coordinate plane, the affine type (ellipse, parabola, hyperbola) of ${\displaystyle E(T,P)}$ is determined by the trace and determinant of the matrix component of ${\displaystyle T}$, independent of ${\displaystyle P}$.

By contrast, the collineation group of the real hyperbolic plane ${\displaystyle \mathbb {H} ^{2}}$consists of isometries. Consequently, the intrinsic conics comprise a small but varied subset of the general conics, curves obtained from the intersections of projective conics with a hyperbolic domain. Further, unlike the Euclidean plane, there is no overlap between the direct ${\displaystyle E(T,P);}$ ${\displaystyle T}$ preserves orientation – and the opposite ${\displaystyle E(T,P);}$ ${\displaystyle T}$ reverses orientation. The direct case includes central (two perpendicular lines of symmetry) and non-central conics, whereas every opposite conic is central. Even though direct and opposite central conics cannot be congruent, they are related by a quasi-symmetry defined in terms of complementary angles of parallelism. Thus, in any inversive model of ${\displaystyle \mathbb {H} ^{2}}$, each direct central conic is birationally equivalent to an opposite central conic.^[8] In fact, the central conics represent all genus 1 curves with real shape invariant ${\displaystyle j\geq 1}$. A minimal set of representatives is obtained from the central direct conics with common center and axis of symmetry, whereby the shape invariant is a function of the eccentricity, defined in terms of the distance between ${\displaystyle P}$ and ${\displaystyle T(P)}$. The orthogonal trajectories of these curves represent all genus 1 curves with ${\displaystyle j\leq 1}$, which manifest as either irreducible cubics or bi-circular quartics. Using the elliptic curve addition law on each trajectory, every general central conic in ${\displaystyle \mathbb {H} ^{2}}$decomposes uniquely as the sum of two intrinsic conics by adding pairs of points where the conics intersect each trajectory.^[9]

Notes

References

Wikimedia Commons has media related to Steiner conic.